Главная
59. Бесшарнирные арки
Бесшарнирная арка представляет собой жестко заделанный с двух концов криволинейный стержень (рис.59.1)
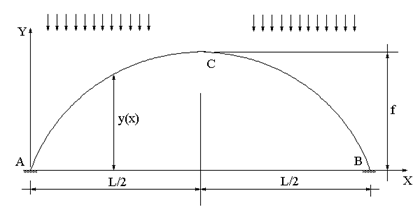
Рис.
59.1
Такая арка является три раза статически неопределимой. Действительно, в ее опорах возникают шесть реакций - две вертикальных, две горизонтальных и два момента, а уравнений равновесия для арки можно составить только три.
Как показал опыт расчета, наибольшие
внутренние усилия и напряжения в арках такого типа возникают вблизи опор.
Поэтому бесшарнирные арки часто конструируют таким
образом, чтобы жесткость на опорах была выше, чем в центре пролета (рис. 59.2).
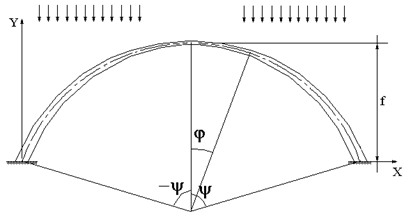
Рис.
59.2
Например, для арок кругового очертания закон изменения момента инерции сечения по длине криволинейного стержня можно задать следующим:
где 
- момент
инерции сечения на оси симметрии арки, n
- некоторый положительный параметр. Очевидно, при n=0 жесткость арки оказывается постоянной по ее длине.
Расчет бесшарнирной
арки также выполняется методом сил. Основная система образуется отбрасыванием
трех связей на оси арки, т.е. фактически рассеканием арки по оси (рис. 59.3).
Влияние отброшенных связей заменяется соответствующими лишними неизвестными 
.
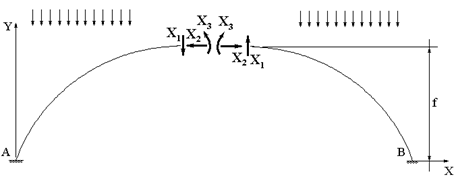
Рис.
59.3
Выражения для изгибающих моментов во вспомогательных состояниях для арки кругового очертания (рис. 59.4 - рис. 59.6) примут вид:
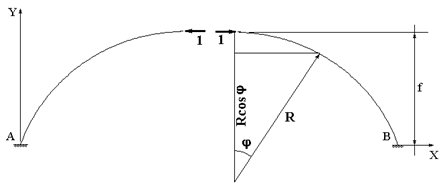
Рис.
59.4
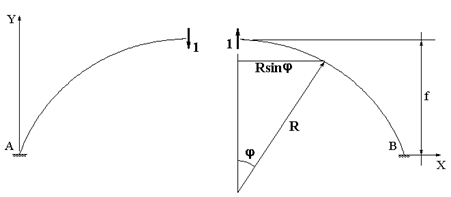
Рис.
59.5
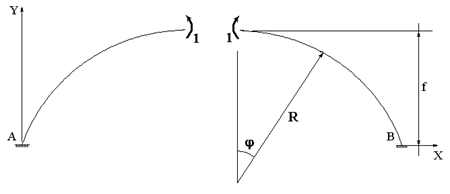
Рис.
59.6
Соответственно, для коэффициентов системы разрешающих уравнений метода сил получим следующие формулы:
Не выполняя вычислений, можно сказать, что
коэффициенты 
и 
равны
нулю. Действительно, эти значения получаются путем перемножения по формулам
Максвелла-Мора симметричной и обратно симметричной эпюр.
После определения (например, численного) значений всех вышеприведенных коэффициентов, формируется и решается система из трех канонических уравнений метода сил:
Затем, после того, как становятся известными
значения находятся окончательные значения изгибающего
момента в сечениях арки:
Реакции в опорах находятся из уравнений
равновесия для левой и правой частей
арки, после того, как удалось найти значения , а эпюры перерезывающего и продольного
усилий определяются по формулам 
и 
.
В качестве примера рассмотрим бесшарнирную арку (рис.59.6) с теми же геометрическими и жесткостными характеристиками и находящуюся под действием той же нагрузки, что и двухшарнирная арка, рассмотренная в предыдущем пункте.
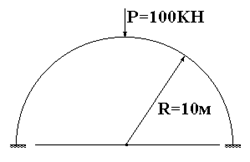
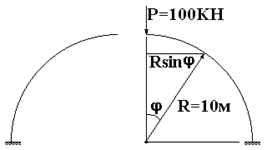
Рис.
59.6 Рис. 59.7
Построим грузовое состояние для основной системы. Как известно, если сосредоточенная сила приложена в точке, через которую выполняется сечение стержня, точку приложения силы перемещают в любую сторону на бесконечно малую величину от точки ее приложения. Переместим ее, например, вправо. Тогда нагрузка будет приложена только к правой половине арки (рис. 59.7), а выражения для изгибающего момента в грузовом состоянии будут следующими:
- для левой половины арки (
): 
- для правой половины арки (
): 
Поскольку жесткость арки является постоянной, внутренние усилия в ней не будут зависеть от нее. Следовательно, значение EJ можно задать, например, равным единице.
В результате вычислений вышеприведенных интегралов Максвелла-Мора с помощью пакета MathCad получаются следующие значения коэффициентов системы разрешающих уравнений метода сил:
Решением системы уравнений являются значения:
Найдем теперь реакции опор в исходной задаче. Рассмотрим левую часть арки (рис. 59.8).
Из уравнений равновесия найдем:
кН,
кН,
кН∙м.
В силу симметрии задачи реакции в правой опоре арки будут такими же.
Далее, по формуле 
определим изгибающие моменты, а по формулам и -
перерезывающее и продольное усилия в сечениях арки. Результаты расчетов для
левой половины арки сведены в таблицу 59.1. На правой половине эпюры
достраиваются исходя из симметричности задачи.
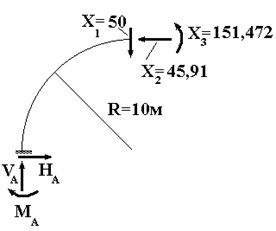
Рис.
59.8
Таблица 59.1
|
Угол град. |
Изгибающий момент
|
Перерезывающее усилие
|
Продольное усилие |
|
-90 |
110,572 |
-45,91 |
-50 |
|
-75 |
8,785 |
-31,405 |
-60,179 |
|
-60 |
-51,991 |
-14,759 |
-66,256 |
|
-45 |
-67,614 |
2,892 |
-67,819 |
|
-30 |
-37,020 |
20,346 |
-64,759 |
|
-15 |
37,706 |
36,414 |
-57,287 |
|
0 |
151,472 |
50,00 |
-45,91 |
Эпюры внутренних усилий в арке приводятся на рис. 59.9 - рис. 59.11.
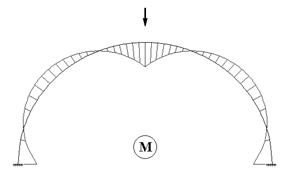
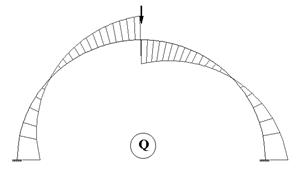
Рис.
59.9 Рис. 59.10
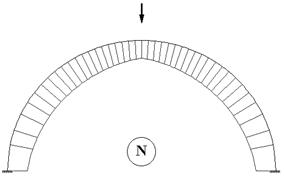
Рис.
59.11
На эпюрах хорошо видно, что вблизи заделок имеет место значительный рост абсолютных значений изгибающего момента, что является характерным для арок такого типа.
email: KarimovI@rambler.ru Адрес: Россия, 450071, г.Уфа, почтовый ящик 21
