Главная

65.6. Устойчивость рам при действии узловых
нагрузок. Метод перемещений. Примеры расчета

Допустим, что рассчитывается следующая рама (рис. 65.11,а). В итоге расчета рамы на прочность будут определены ее внутренние усилия, в частности, ее продольные усилия (рис. 65.11,б). Если они сжимающие и большие, существует опасность потери устойчивости рамы. Поэтому раму следует рассчитывать и на устойчивость от действия сжимающих усилий (рис. 65.11,в). В некоторых случаях может ставиться задача проверки устойчивости рамы при узловом воздействии нагрузки (рис. 65.11,г).

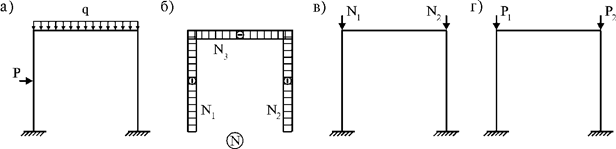
Рис. 65.11

Обе эти задачи можно решать методами сил или перемещений. Остановимся на методе перемещений и примем следующие гипотезы:

– нагрузка прикладывается только в узлах;

– продольные силы вызывают только центральное сжатие;

– при потере устойчивости напряжения остаются в упругой зоне;

– деформации малы, а расстояния между узлами сохраняются.

Эти гипотезы позволяют вести расчет рам на устойчивость по единой методике. Ее начальные этапы совпадают с обычным методом перемещений, а в дальнейшем их порядок и сущность меняются.

Напомним: в методе перемещений в качестве неизвестных принимаются линейные и угловые перемещения Z_i. При расчете на устойчивость по методу перемещений выбор основной системы не отличается от выбора основной системы при обычном статическом расчете этим методом.

Общий вид канонических уравнений представим на примере с 3-мя неизвестными:

;

;

.

где – неизвестные угловые и линейные перемещения; – коэффициенты метода перемещений, которые зависят от продольных усилий в стержнях; n – число введенных связей в основной системе.

Всю нагрузку, действующую на конструкцию (сооружение) (рис. 65.12,б), распределяем по узлам. Тогда реактивные усилия во введенных связях от внешней нагрузки будут равны нулю и система канонических уравнений становится однородной, т. е.:

;

;

.

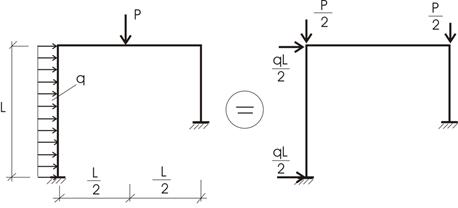
Рис.65.12

Такая система уравнений имеет два решения:

1) либо Z_i =0, т. е. перемещения узлов отсутствуют;

2) либо определитель системы уравнений равен нулю:

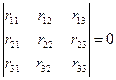(1)

Первый случай нас не устраивает, поскольку нет перемещений – нет и вопроса устойчивости, т. к. только при наличии перемещений узлов происходит потеря устойчивости конструкции.

Остается второй случай:

Det=0.

Раскрытие детерминанта приводит к уравнению, называемому уравнением устойчивости. Дальнейшее решение задачи состоит в отыскании значений нагрузок на раму, удовлетворяющих уравнению Det=0. Наименьшая из них будет критической нагрузкой.

Коэффициенты в определителе вычисляются как в методе перемещений из эпюр моментов при единичных перемещениях введенных связей, но с учетом продольного воздействия сжимающей силы .

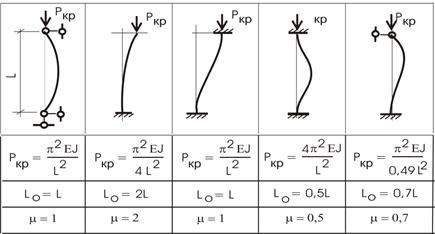
Для отдельных стержней с различными условиями опирания эти задачи решены и представлены в таблице 1.

Таблица 1. Реакции стержней постоянного сечения при действии сжимающих

осевых сил и при перемещениях одного из концов стержня.

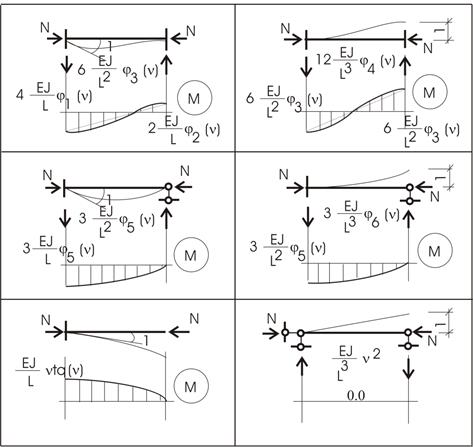
Если присмотреться к величинам реактивных усилий, то заметим, что к известному значению от перемещения без влияния продольной силы добавляется сомножитель, учитывающий влияние сжимающих усилий. Значения этих функций имеют вид:

; ; ;

; ; .

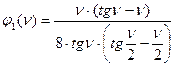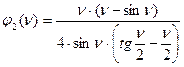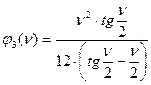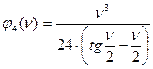Функции зависят от критического параметра , который вычисляется по формуле

,

где - длина -го стержня; .

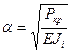Определив все в общем виде, подставим их в определитель. Раскроем определитель и получим уравнение устойчивости, решение которого производится методом подбора с использованием таблицы 3. Для этого назначается начальная величина , по которой определяются значения и т. д. Полученные значения подставляются в уравнение устойчивости. Если результат вычислений не равен нулю при заданном значении , то принимается новое значение и до тех пор, пока уравнение не достигнет нуля (или будет близким к нулю). Последнее значение и есть тот критический параметр, соответствующий критической силе .

По величине подбирается (или проверяется) длина стержня по выражению:

.

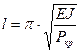Расчетная же длина стержня определяется из соотношения:

,

где μ – коэффициент, зависящий от условий закрепления концов стержня (табл. 2).

Таблица 2

65.7. Примеры расчета рамы на устойчивость

Пример 1. Определить величину критической силы для стойки (рис. 65.13,а) постоянной жесткости .

Решение. Основная система метода перемещений для стойки показана на рис. 65.13,б.

Эпюра моментов от единичного перемещения связи (угла поворота введенной заделки) с использованием таблицы 1 показана на рис. 65.13,в. Каноническое уравнение запишется:

.

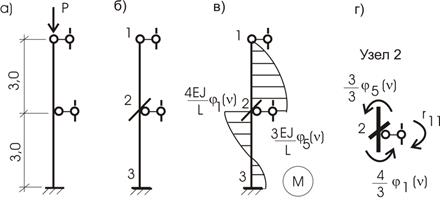
Рис.65.13

Критический параметр для обоих участков (стержней) одинаковый:

;

l = 3; следует найти, (по условию задачи).

Величина вычисляется из условия равновесия узла 2 (рис. 65.13,г):

.

Уравнение устойчивости примет вид:

или

.

Данное уравнение решаем путем подбора, используя таблицу 3 специальных функций.

Исследуя данное уравнение, замечаем, что одно из слагаемых должно быть величиной отрицательной. Из таблицы видим, что при малых значениях () отрицательной будет функция .

1) Принимаем .

; .

Подставим их в уравнение устойчивости:

.

2) Примем .

; ;

.

Решение находится между , но ближе к 3,6 (по интерполяции).

Таблица 3

0,0	1,0000	1,0000	1,0000	1,0000	1,0000	1,0000
0,1	0,9997	1,0002	0,9998	0,9990	0,9993	0,9960
0,2	0,9987	1,0007	0,9993	0,9960	0,9973	0,9840
0,3	0,9970	1,0015	0,9985	0,9910	0,9940	0,9640
0,4	0,9947	1,0027	0,9973	0,9840	0,9893	0,9360
0,5	0,9916	1,0042	0,9958	0,9750	0,9832	0,8999
0,6	0,9879	1,0061	0,9940	0,9640	0,9757	0,8557
0,7	0,9836	1,0083	0,9918	0,9510	0,9669	0,8035
0,8	0,9785	1,0109	0,9893	0,9360	0,9565	0,7432
0,9	0,9727	1,0138	0,9864	0,9189	0,9447	0,6747
1,0	0,9662	1,0172	0,9832	0,8999	0,9313	0,5980
1,1	0,9590	1,0209	0,9797	0,8788	0,9164	0,5131
1,2	0,9511	1,0251	0,9757	0,8557	0,8998	0,4198
1,3	0,9424	1,0297	0,9715	0,8307	0,8814	0,3181
1,4	0,9329	1,0348	0,9669	0,8035	0,8613	0,2080
1,5	0,9227	1,0403	0,9619	0,7744	0,8393	0,0893
π/2≈1,57	0,9149	1,0445	0,9581	0,7525	0,8225	0,0000
1,6	0,9116	1,0463	0,9565	0,7432	0,8152	–0,0381
1,7	0,8998	1,0529	0,9508	0,7100	0,7891	–0,1743
1,8	0,8871	1,0600	0,9447	0,6747	0,7606	–0,3194
1,9	0,8735	1,0676	0,9382	0,6374	0,7297	–0,4736
2,0	0,8590	1,0760	0,9313	0,5980	0,6961	–0,6372
2,1	0,8436	1,0849	0,9241	0,5566	0,6597	–0,8103
2,2	0,8273	1,0946	0,9164	0,5131	0,6202	–0,9931
2,3	0,8099	1,1051	0,9083	0,4675	0,5772	–1,1861
2,4	0,7915	1,1164	0,8998	0,4198	0,5304	–1,3896
2,5	0,7720	1,1286	0,8908	0,3700	0,4793	–1,6040
2,6	0,7513	1,1417	0,8814	0,3181	0,4234	–1,8299
2,7	0,7295	1,1559	0,8716	0,2641	0,3621	–2,0679
2,8	0,7064	1,1712	0,8613	0,2080	0,2944	–2,3189
2,9	0,6819	1,1878	0,8505	0,1497	0,2195	–2,5838
3,0	0,6560	1,2057	0,8393	0,0893	0,1361	–2,8639
3,1	0,6287	1,2251	0,8275	0,0267	0,0424	–3,1609
π ≈3,14	0,6168	1,2337	0,8225	0,0000	0,0000	–3,2899
3,2	0,5997	1,2462	0,8152	–0,0381	–0,0635	–3,4769
3,3	0,5691	1,2691	0,8024	–0,1051	–0,1847	–3,8147
3,4	0,5366	1,2940	0,7891	–0,1743	–0,3248	–4,1781
3,5	0,5021	1,3212	0,7751	–0,2457	–0,4894	–4,5727
3,6	0,4655	1,3509	0,7606	–0,3194	–0,6862	–5,0062
3,7	0,4265	1,3834	0,7455	–0,3954	–0,9270	–5,4904
3,8	0,3850	1,4191	0,7297	–0,4736	–1,2303	–6,0436
3,9	0,3407	1,4584	0,7133	–0,5542	–1,6269	–6,6969
4,0	0,2933	1,5019	0,6961	–0,6372	–2,1726	–7,5060
4,1	0,2424	1,5501	0,6783	–0,7225	–2,9802	–8,5836
4,2	0,1878	1,6037	0,6597	–0,8103	–4,3156	–10,196
4,3	0,1287	1,6636	0,6404	–0,9005	–6,9947	–13,158
4,4	0,0648	1,7310	0,6202	–0,9931	–15,327	–21,780
4,4934	0,0000	1,8017	0,6006	–1,0820	–∞/+∞	–∞/+∞
4,5	–0,0048	1,8070	0,5991	–1,0884	227,93	221,18
4,6	–0,0809	1,8933	0,5772	–1,1861	14,669	7,6160
4,7	–0,1645	1,9920	0,5543	–1,2865	7,8186	0,4553
3 π /2≈4,71	–0,1755	2,0051	0,5514	–1,2991	7,4038	0,0000
4,8	–0,2572	2,1056	0,5304	–1,3896	5,4023	–2,2777
4,9	–0,3607	2,2375	0,5054	–1,4954	4,1463	–3,8570
5,0	–0,4772	2,3923	0,4793	–1,6040	3,3615	–4,9719
5,1	–0,6099	2,5757	0,4520	–1,7155	2,8130	–5,8570
5,2	–0,7629	2,7960	0,4234	–1,8299	2,3986	–6,6147
5,3	–0,9422	3,0648	0,3935	–1,9474	2,0668	–7,2965
5,4	–1,1563	3,3989	0,3621	–2,0679	1,7884	–7,9316
5,5	–1,4182	3,8236	0,3291	–2,1917	1,5455	–8,5379
5,6	–1,7481	4,3794	0,2944	–2,3189	1,3266	–9,1268
5,7	–2,1803	5,1346	0,2580	–2,4495	1,1235	–9,7065
5,8	–2,7777	6,2139	0,2195	–2,5838	0,9302	–10,283
5,9	–3,6679	7,8727	0,1790	–2,7219	0,7421	–10,861
6,0	–5,1594	10,727	0,1361	–2,8639	0,5551	–11,444
6,1	–8,2336	16,739	0,0907	–3,0102	0,3656	–12,037
6,2	–18,590	37,308	0,0424	–3,1609	0,1700	–12,643
2 π ≈6,28	–∞	+∞	0,0000	–3,2899	0,0000	–13,159

Примем .

или ,

откуда

.

Расчетные длины стержней для обоих участков будут равны (используется табл. 2):

(м).

Пример 2. Определить величину критической силы для рамы, приведенной на рисунке 65.14,а.

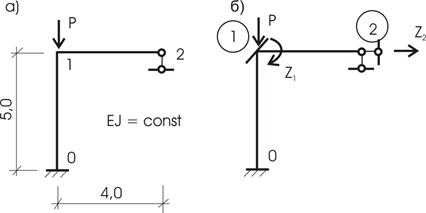
Рис.65.14

Решение.

.

Здесь мы опускаем процесс подсчета числа неизвестных.

Основная система показана на рисунке 65.14,б.

Система канонических уравнений запишется:

.

В этой системе должно быть . Тогда должен равняться нулю определитель при неизвестных, т. е.

.

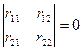Раскроем определитель:

.

Произведем вычисления .

Эпюры М₁ и М₂ (от единичных перемещений первой и второй связей соответственно) приведены на рисунке 65.15,а,б.

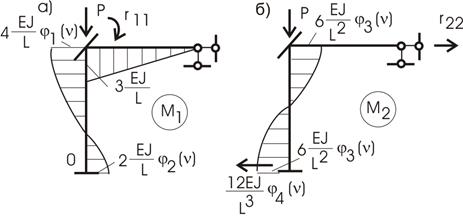
Рис.65.15

Напоминаем: для сжатых стержней внешней нагрузкой (в нашем случае только стойка) эпюра изгибающих моментов берется из таблицы 1, а для стержней, не подвергающихся сжатию, принимается, как и в обычном методе перемещений.

Из эпюры М₁ вырежем узел с первой связью (рис. 65.16 и здесь же показано вычисление r₁₁).

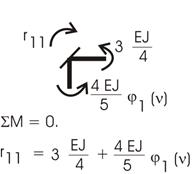
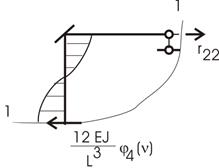
Рис.65.16 Рис.65.16

Из эпюры М₂ сечением 1 – 1 определим (рис. 65.16).

; ; .

Вырезая узел с первой связью (рис. 65.17), находим :

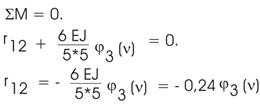
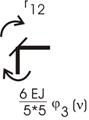
Рис.65.17

Подставим полученные значения в уравнение устойчивости:

.

Вынесем EJ. Получаем:

.

В полученном уравнении параметр устойчивости один (т.е. для одного стержня).

Переходим к решению уравнения.

Принимаем , тогда по таблице 3:

.

Подставим в уравнение устойчивости:

D = .

Принимаем :

D = .

Принимаем :

D = .

Значение критического параметра находится между и с большим приближением к .

Интерполируя, принимаем .

Критическая сила определится:

.

Расчетная длина сжатого стержня, а именно стержня 0-1, определится:

.

Пример 3. Для заданной рамы и приложения нагрузки определить величину и расчетные длины сжатых стержней (рис. 65.18,а).

Определяем основную систему метода перемещений (рис. 65.18,б). Получим раму с 3-мя неизвестными. Определитель системы канонических уравнений при неизвестных приравняем нулю.

;

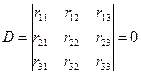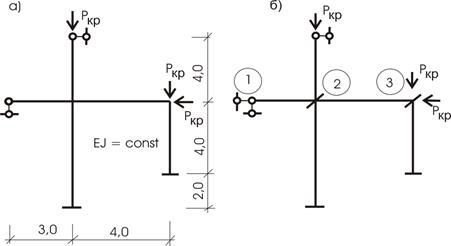
Рис.65.18

Раскроем определитель по элементам первой строки и приравняем результат раскрытия определителя нулю, т. е. получим уравнение устойчивости:

.

Для вычисления построим эпюры изгибающих моментов от перемещений введенных связей на единицу, используя таблицу 1 для сжатых стержней (рис. 65.19 и 65.20).

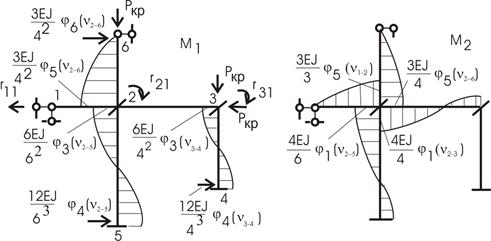
Рис.65.19

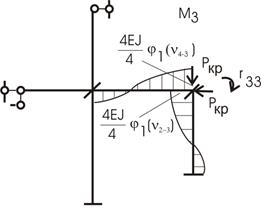
Рис.65.20

Из полученных эпюр видим, что критический параметр для стержней различный. Приведем их к одному, т.е. получим так называемые приведенные параметры .

Распишем критические параметры для каждого стержня из общего выражения:

,

где, как мы уже отмечали, .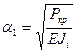

При . С учетом этого запишем:

.

Примем больший критический параметр за (можно сказать, за единичный). Тогда все другие, заметьте, будут выражаться через с коэффициентом меньшим единицы, а именно:

.

(Отметим, что это делается лишь для того, чтобы при использовании таблицы 3 не получилось так, что значения критического параметра в ней не окажется).

Вернемся к вычислению реактивных усилий - .

Из эпюры М₁ находим :

;

;

.

Из эпюры М₂ находим :

;

.

Из эпюры определим :

.

Выпишем отдельно значения , входящие в уравнение устойчивости:

;

;

;

;

;

и рядом запишем само уравнение:

.

Значение критического параметра вычисляется из выражения:

,

где, как нам известно, зависит от закрепления концов сжатого стержня (см. таблицу 2). Для первого стержня , а для последнего -. Следовательно, значение критического параметра лежит в пределах от 3,14 до 4,49. В первом приближении примем = 3.

0,666 = 2,0; 0,5 = 1,5.

По таблице 3 определяем значения функций:

; ;

; ;

;

; ;

; ;

.

Теперь вычислим :

;

;

; ;

; .

Полученные значения подставляем в уравнение равновесия:

.

Как видим, результат не равен нулю.

Положим ,90; 0,666 =2,6; 0,5 = 1,95 .

Значения функций:

; ;

; ;

;

; ;

; ;

.

Вычисляем (промежуточные вычисления опускаем):

; ;

; ;

; .

Вычисляем само уравнение:

.

Интерполяция в предположении линейности уравнения дает = 3,16.

По условию закрепления стержней (табл. 5) вычисляем их расчетные длины, т.е.:

; ;

; ;

.

Используя расчетные длины стержней и критический параметр для них, определяем величину критических усилий (критическую нагрузку) для каждого стержня из выражения:

.

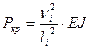Тогда

,

а далее запишем только результаты:

Р_2-3 = 1,102ЕJ; Р_2-6 = 0,127EJ;

Р_2-5 = 0,277EJ; Р_3-4 = 0,275EJ.

Пример 4. Для заданной рамы, изображенной на рис.65.21,а, предполагая, что EI_p = 2EI_{c ;} l = 4 м; EI_c = 4000 кНм², требуется:

1. Показать возможные формы потери устойчивости рассматриваемой системы;

2. Определить критические значения силы Р₁ и Р₂ для случаев:

а) Р₁ = Р; Р₂ =0; б) Р₁ = Р₂ = Р; в) Р₁ = 0; Р₂ = Р.

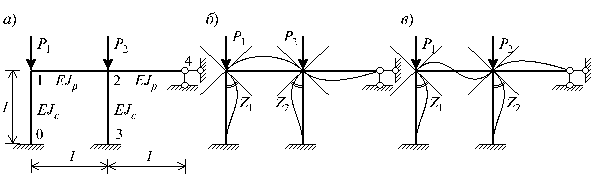
Рис.65.21

Решение:

1. Показать возможные формы потери устойчивости рассматриваемой рамы

Рассматриваемая система является дважды кинематически неопределимой. Возможные формы потери устойчивости системы определяются угловыми перемещениями узлов 1 и 2. Следовательно, для установления искривленной формы рамы необходимо определить углы поворотов Z₁ и Z₂ двух смежных узлов 1 и 2.

В критическом состоянии возможные формы потери устойчивости изображены на рис.65.21,б, в.

2. Определить критические значения силы Р₁  и Р₂ для случаев: а) Р₁ = Р; Р₂ =0 ; б) Р₁ = Р₂ = Р; в) Р₁ = 0; Р₂ = Р

Приступая к решению поставленной задачи, в качестве базовой принимаем стойку 0-1 с изгибной жесткостью ЕJ_c = 4000 кН∙м² и длиной l = 4 м.

Вычисляем погонные изгибные жесткости элементов рассматриваемой рамы:

кН×м;

кН×м.

Введем обозначения: кНм; ; .

Случай а): Р₁ = Р; Р₂ =0.

Последовательно задавая перемещения Z₁ = 1, Z₂ = 1 и пользуясь табл.1, строим единичные эпюры М₁ и М₂, выражая ординаты эпюры моментов М₁ и М₂ через величину i (рис.65.22, а, б).

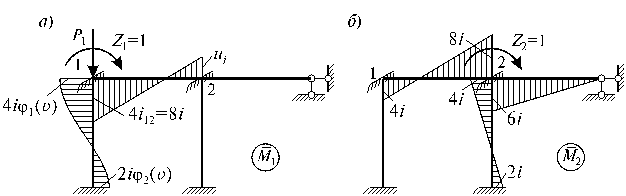
Рис.65.22

В соответствии с методом сечений вырезаются узлы 1 и 2 (рис.65.22) и из условий их равновесия определяются выражения реактивных моментов:

; ; .

Уравнение устойчивости принимает вид:

,

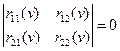откуда ,

или .

Из решения последнего уравнения получим:

Применяя принцип линейного интерполирования, с помощью табл.3 вычисляем значение параметра:

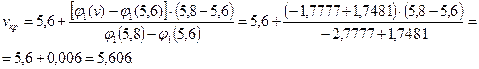
Критическая сила будет

кН.

Случай б): Р₁ = Р₂ = Р;

Эпюры моментов М₁ и М₂ в данном случае принимают вид (рис.65.23).

В соответствии с методом сечений вырезаются узлы 1 и 2 (рис.65.23) и из условий их равновесия определяются выражения реактивных моментов (i,k = 1,2):

; ; .

Подставляя выражения (i,k = 1,2) в уравнение устойчивости, получим:

.

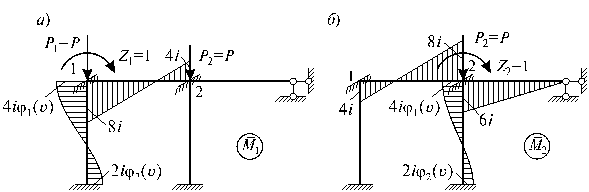
Рис.65.23

Из решения последнего уравнения получим:

или ; ,

Применяя принцип линейного интерполирования, по заданным значениям (табл.3) определяем минимальное значение параметра критической нагрузки:

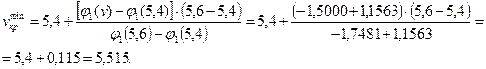
Следовательно,

кН.

Случай в): Р₁ = 0; Р₂ = Р.

В этом случае эпюры моментов М₁ и М₂ имеют вид, изображенный на рис.65.24.

Рис.65.24

Выражения реактивных моментов в данном случае имеют вид:

; ; .

Из уравнений устойчивости получим

.

Из решения последнего уравнения получим:

.

Из табл.3 применяя принцип линейной интерполяции вычисляем значение параметра v:

.

Критическая сила будет

кН.

Обобщая результаты расчетов величин критических сил в зависимости от вида нагружения рамы, имеем:

а) Р₂ = 0; P_1,кр = 7856,1 кН;

б) P_1,кр = P_2,кр = 7604 кН;

в) P₁ = 0; P_2,кр = 8505,9 кН.

Откуда следует, что при P₁ = P₂ критическое значение силы P_кр меньше наименьшего значения критической силы в случае, если на систему действовала бы приложена только одна из сил P₁ или P₂, т.е. 7604 кН < 7856,1 кН.

Резюмируя, заметим, что как это показывают результаты расчетов, наступление критического состояния системы зависит как от свойств заданной системы, так и от схемы нагружения.

В рассматриваемом примере, как это следовало бы ожидать, наиневыгоднейшей схемой нагружения является схема б), т.е. когда одновременно в каждом из двух узлах заданной системы приложены одинаковые силы.

Далее, сравнивая случаи нагружения а) и в), легко установить, что из этих двух случаев нагружения, случай а) является более опасным для заданной системы, т.к. в этом случае потеря устойчивости наступает при более низком уровне величины внешней силы.

Данное обстоятельство объясняется тем, что жесткость узла под номером 1 заданной системы, меньше по сравнению с жесткостью узла под номером 2, т.к. жесткость первого узла формируется двумя элементами (стойки и одного ригеля), а жесткость второго узла формируется тремя элементами (идентичной стойкой, левым ригелем, который является общим для формирования жесткости первого и второго узла, а также правым ригелем).

Пример 5. Найти критическую силу для рамы с одной сжатой стойкой, представленной на рис. 65.25, где указаны размеры и жесткости элементов рамы.

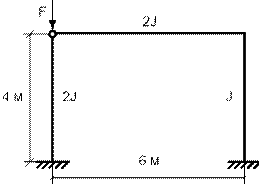
Рис. 65.25

Решение. Число лишних неизвестных равно двум: угол поворота жесткого узла и линейное горизонтальное смещение ригеля.

На рис. 65.26 показаны основная система, единичная эпюра и ее характерные ординаты.

Ординаты определены согласно данным таблицы 1.

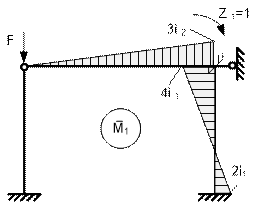
Рис. 65.26

На рис. 65.27 представлена единичная эпюра и ее характерные ординаты.

Погонные жесткости стержней ,

где n – кратность жесткости стержня.

Следовательно,

.

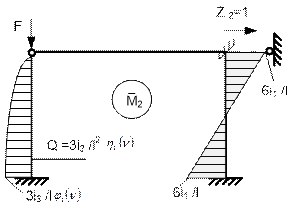
Рис. 65.27

Используя данные эпюр (см. рис. 65.26), (рис. 65.27) и табл.1, определим коэффициенты

.

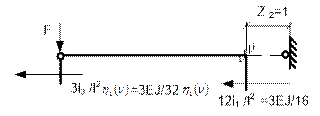
Рис. 65.28

Коэффициент r₂₂ определяют исходя из схемы равновесия ригеля (рис. 65.28):

Подставив коэффициенты в определитель (1) и сократив все члены на EJ, получим

При раскрытии определителя, функция влияния продольной силы имеет вид

По табл.3 находим критический параметр v=2,35.

Таким образом, критическая сила будет равна:

Пример 6. Рама с сжатой стойкой жесткого узла. Определить критическую силу для сжатой стойки рамы, показанной на рис.65.29 с указанными жесткостями стержней и их размерами.

В отличие от предыдущего примера продольная сила приложена в жестком узле. Число лишних неизвестных также равно двум.

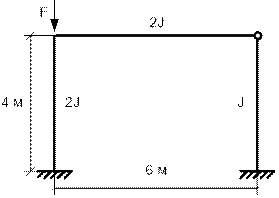
Рис. 65.29

Решение. Основная система и эпюры моментов от единичных смещений показаны на рис. 65.30 и рис.65.31. Построение этих эпюр произведено в соответствии с данными табл.1.

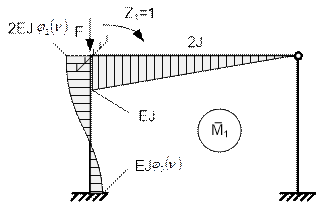
Рис. 65.30

Коэффициенты канонических уравнений:

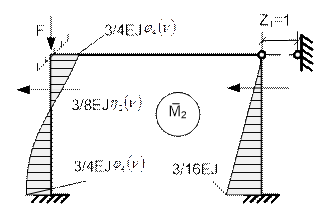
Рис. 65.31

Подставим коэффициенты в определитель.

Раскрытый определитель, в соответствие с выражением (2), представляет трансцендентное уравнение (так называемое уравнение устойчивости).

Открывая его методом подбора, найдем минимальное значение критического параметра v:

Или в раскрытом виде имеем:

Далее необходимо найти такое значение параметра v, при котором определитель обратится в нуль. Параметр v изменяется в пределах ().

Задаем значения, близкие к среднему, . Определяем функции учета продольных сил согласно табл.3. Данные приведены в табл. 4.

Таблица 4

v				D
2	0,8590	0,9311	0,5980	2,718 -0,6983 -0,6983 0,2713 = 0,2497
3	0,6560	0,8393	0,0893	1,312 -0,6295 -0,6295 0,0893 = -0,2906

Построим график зависимости D от v методом линейной интерполяции (рис. 8). Находим v, близкое к фактическому. При v=2,42 определитель (2) превращается в ноль.

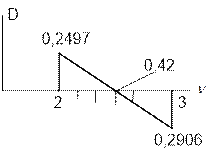
Рис. 65.32

Таким образом, критическая сила будет равна:

Пример 7. Рама с шарнирным закреплением ригеля. На рис. 65.33 показана рама с двумя сжатыми стойками. Найдем критические силы при заданных размерах и жесткостях элементов.

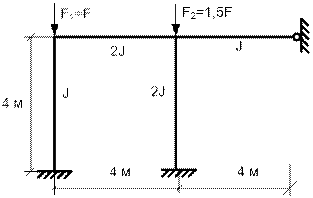
Рис. 65.33

Основная система изображена на рис. 65.34.

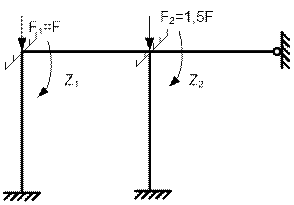
Рис. 65.34

На рис.65.35 и рис.65.36 представлены единичные эпюры моментов от поворотов жестких узлов рамы на и .

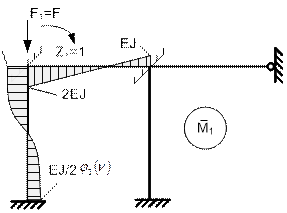
Рис.65.35

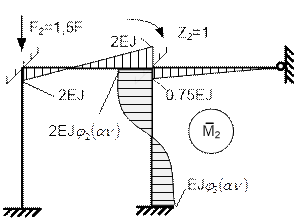
Рис. 65.36

Критические силы для каждой стойки будут различны, следовательно, критические параметры (с учетом коэффициента приведения) соответственно равны:

– для первой стойки

– для второй стойки

Уравнение устойчивости запишем в следующем виде:

Решение такого уравнения следует проводить путем подбора.

Прежде следует задаться начальным параметром v. Подставим значения функций в уравнение (3) и определим в каких пределах его можно изменять. Обе стойки рамы находятся в таких условиях, что их верхние концы не могут смещаться горизонтально, но упруго поворачиваются в узлах. Следовательно, критические силы стоек будут близки к критической силе прямолинейного стержня с заделкой обоих концов. Критический параметр в этом случае .

Первоначально примем значение критического параметра в пределах . Согласно табл. 5 имеем два значения функций

Таблица 5

v			D
5	-0,4772	0,1285	1,5228 1 1 3,2614 = 4,3831
6	-5,1589	-0,763	-5,1589 1 1 1,987 = -9,2504

Построим график зависимости D от v и методом линейной интерполяции (рис. 65.37) находим v. При v=5,32 уравнение (3) обращается в ноль.

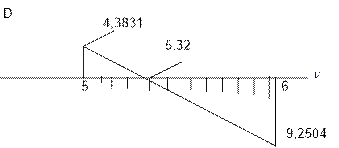
Рис. 65.37

Следовательно, критические силы равны:

– для первой стойки

– для второй стойки

Пример 8. Трехстоечная рама с загружением в шарнирных узлах. Рассмотрим пример определения критических сил для рамы, представленной на рис. 65.38. Основная система изображена на рис. 65.39.

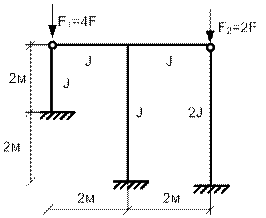
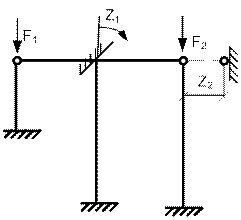
Рис. 65.38 Рис. 65.39

Решение. Критические параметры для каждой стойки равны:

– для первой стойки

– для второй стойки

Эпюры единичных моментов изображены на рис.65.40 и рис.65.41.

Коэффициенты уравнения устойчивости:

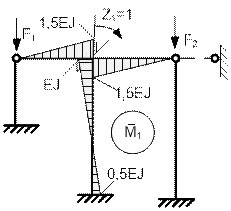
Рис.65.40

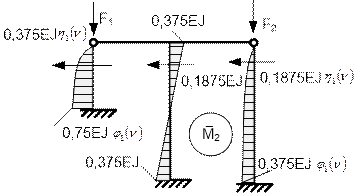
Рис.65.41

Уравнение устойчивости запишем в следующем виде:

Раскрытие его приводит к простому уравнению:

.

Отсюда находим v=1,45 и

Пример 9. Трехстоечная рама с загружением центральной и крайней стоек. На рис. 65.42 изображена рама с двумя сжатыми стойками с заданными размерами и жесткостями элементов.

Решение. Основная система дана на рис. 65.43.

Критические параметры:

– для первой стойки

– для второй стойки

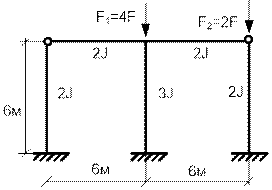
Рис. 65.42

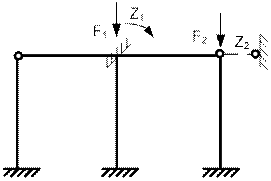
Рис. 65.43

Единичные эпюры моментов от поворота жесткого узла на и линейного смещения узлов ригеля на показаны на рис. 65.44 и рис.65.45.

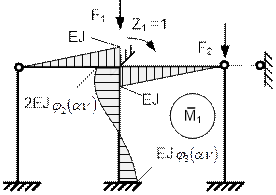
Рис. 65.44

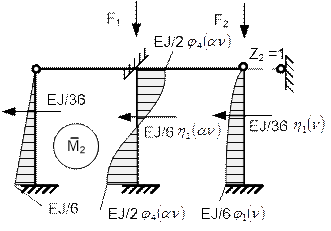
Рис. 65.45

Коэффициенты уравнения устойчивости:

Определитель уравнения устойчивости:

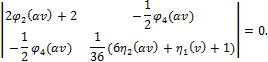
Раскрыв определитель, получим трансцендентное уравнение, которое решается путем подбора критического параметра v.

Примем значение критического параметра v в следующим пределе: .

Критический параметр для коэффициентов умножается на .

Согласно табл. 6 определяем критические параметры и значения определителя D.

Таблица 6

v					D
2	0,8099	0,9083	-1,1861	0,598	3,6198 -0,4542 -0,4542 0,0945 = 0,1358
3	0,5194	0,7821	-2,8639	-0,2100	3,0388 -0,3911 -0,3911 -0,0576 = -0,2227

Построим график изменения величин D при v=2 и D при v=3, считая их изменяющимися по линейной зависимости (см. рис. 65.46).

Сближая постепенно границы между , получим искомую величину v=2,35, при которой определитель D=0.

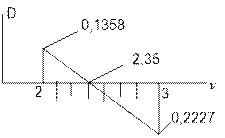
Рис. 65.46

Таким образом, критические силы равны:

– для первой стойки

– для второй стойки

Пример 9. Рама с двумя крайними шарнирами. На рис. 65.47 изображена рама с двумя сжатыми крайними стойками, верхние концы которых шарнирные.

Решение. Возможен случай, когда стойки будут выпучиваться, а средняя стойка остается недеформированной. В этом случае критическая сила будет равна:

Возможен также другой вид деформированного состояния, показанный пунктиром на рис.65.47.

Основная система представлена на рис. 65.48.

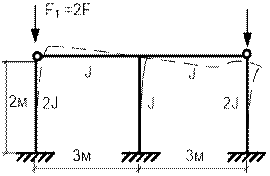
Рис.65.47

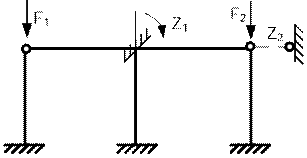
Рис. 65.48

По единичным эпюрам изгибающих моментов (рис. 65.49) и (рис. 65.50) находим:

Определитель уравнения устойчивости:

Приходим к простому уравнению или .

Отсюда, (см. табл.3) v=1,75. Критическая сила при этом равна:

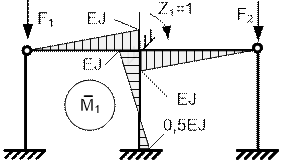
Рис.65.49

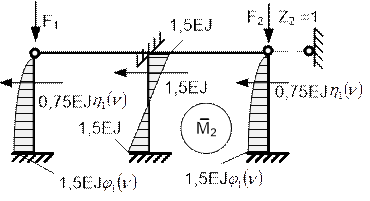
Рис.65.50

Следовательно, наименьшей критической силе соответствует деформированное состояние, показанное пунктиром на рис. 65.47.

---

email: KarimovI@rambler.ru

Адрес: Россия, 450071, г.Уфа, почтовый ящик 21

Теоретическая механика Сопротивление материалов

Прикладная механика Детали машин Теория машин и механизмов

00:00:00