Главная

8.12. Учет и исследование зависимости усилий в статически неопределимых стержневых системах от деформаций

Далее рассматриваются вопросы учета и исследования зависимости усилий в статически неопределимых плоских стерж-невых системах от двух видов деформаций – сдвига при поперечном изгибе элементов и растяжения-сжатия гибких (тонких) стержней. Из методических соображений в каждом из приводимых примеров изучается влияние лишь какого-либо одного из указанных видов деформаций.

8.12.1. Расчет статически неопределимых конструкций с учетом деформации сдвига

Изгиб элементов конструкций редко бывает чистым – обычно он сопровождается сдвигом, в поперечных сечениях кроме нормальных напряжений действуют и касательные . Напряжения и связаны соответственно с интегральными внутренними силовыми факторами – изгибающим моментом M и поперечной силой Q . Их вклад в возникающие полные перемещения определяется для плоских стержневых систем первым и вторым членами формулы Максвелла – Мора ( 6.8 ). Традиционно считается, что влияние сдвига незначительно, и в большинстве обычных расчетов его не принимают во внимание. Вместе с тем достаточно легко убедиться в том, что даже в широко распространенных простых балочных системах пренебрегать сдвигом при определении перемещений (в частности, при проверке выполнения нормативных требований по прогибам конструкции) во многих случаях нельзя, так как погрешность может быть недопустимо большой.

В соответствии с формулой ( 6.8 ) перемещение, обусловленное только деформациями поперечного изгиба самой конструкции (то есть без учета податливости опор и продольных деформаций элементов – полагаем C_j = и EA =), можно представить в виде

, ( 8.69 )

где – часть полного перемещения, обусловленная изгибом (от действия моментов М);

a_Q = D_iF,Q /D_iF,M – относительная поправка за счет сдвига;

– часть полного перемещения, обусловленная сдвигом (от действия поперечных сил Q);

k_t – коэффициент, отражающий неравномерность распределения касательных напряжений t по высоте сечения.

Так как в каждом конкретном случае входящие в подынтегральные выражения силовые факторы в единичном состоянии M_i , Q_i и в грузовом состоянии M_F, Q_F – известные функции, то коэффициент a_Q можно записать так:

, ( 8.70 )

где b_s – коэффициент, определяемый для каждой рассчитываемой системы индивидуально и зависящий от особенностей самой конструкции (ее геометрии, структуры и распределения жесткостей), характера нагрузки и от того, какое именно перемещение находится.

В общем случае величины k_t , E , G , I , A , l нужно понимать как параметры, через которые выражаются однотипные с ними характеристики разных элементов и участков системы (в том числе и переменные вдоль осей стержней).

Если k_t , E, G, I, A постоянные и одинаковые для всех участков, то

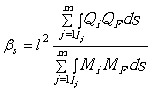. ( 8.71 )

Рассмотрим модельную задачу – однопролетную балку постоянного сечения длиной l. Оценим влияние сдвига на наибольший прогиб балки v_max = D_1F. Выполнив вычисление интегралов в выражении ( 8.71 ) для двух характерных видов нагрузок – равномерно распределенной по всей длине ( q ) и сосредотoченной посредине пролета ( F ) при разных способах закрепления концов балки, получаем значения коэффициента b_s , приведенные в таблице:

Закрепление концов балки	Нагрузка q	Нагрузка F
Шарнирное	48/5	12
Жесткое	48	48

Заметим, что b_s в значительно меньшей степени зависит от характера нагрузки, чем от способа опирания балки – для статически неопределимой системы (при жестком защемлении обоих концов) b_s в 4...5 (!) раз больше, чем при статически определимом шарнирном.

Момент инерции сечения I можно выразить через площадь сечения A и его радиус инерции r: I = Ar², а r представить в отношении к высоте сечения h как r = a_rh , тогда формулу для коэффициента влияния сдвига ( 8.70 ) получим в еще более удобном для анализа виде:

, ( 8.72 )

что позволяет легко выявить основные факторы, от которых зависит поправка на сдвиг. Это:

- особенности системы и нагрузки, учитываемые коэффициентом b_s ;

- физические свойства материала, описываемые отношением модулей упругости – Юнга ( Е ) и сдвига ( G ) ;

- форма и относительные пропорции сечения – от них зависят коэффициент k_t и относительный радиус инерции сечения a_r ;

- высота сечения балки в отношении к ее пролету («массивность» балки).

В следующей таблице приведены значения коэффициентов a_r и k_t для некоторых распространенных типов сечений строительных конструкций (в т.ч. балок).

Тип сечения
Прямоугольное однородное	~0,3	6/5
Стальной прокатный двутавр	~0,4	A/Aw = 2,5 ... 3
Тонкостенный двутавр	~0,45	A/Aw = 3 ... 5

Здесь A_w – площадь сечения стенки двутавра.

Для балок с защемленными концами при вышеуказанных нагрузках и типах сечений a_Q 48(0,3 ... 0,45)²k_t (E/G)(h/l)²(4 ... 10) k_t (E/G)(h/l)².

Наконец, для стальных балок из прокатных двутавров, учитывая, что для однородных изотропных материалов, к которым относятся и строительные стали, E/G = 2(1+n)2,5 (n = 0,2 ... 0,3 – коэффициент Пуассона), получим

a_Q 50(h/l)² , ( 8.73 )

откуда видно, что с увеличением относительной высоты балки влияние сдвига сильно возрастает.

Обычно стальные строительные балки имеют h/l = 1/8 ... 1/12 – для этого интервала по ( 8.73 ) получается a_Q = 0,78 ... 0,35. Для шарнирно опертой балки значения a_Q получаются меньше в 4 ... 5 раз, но и в этом случае поправки к перемещениям, вычисленным без учета влияния сдвига, составят 7 ... 20%, что, конечно, значительно превышает погрешность вычислений, допускаемую в расчетах конструкций.

Для более тонкостенных, чем прокатные двутавры, профилей сечений влияние деформации сдвига сказывается еще больше. Еще одной причиной увеличения сдвиговой податливости конструкции могут быть физические свойства материала, а именно – относительно низкое значение модуля сдвига в сравнении с модулем продольной упругости, что характерно для природно (древесина) или конструктивно (композиты, фанера и др.) анизотропных материалов. Некоторые особенности нагрузок также могут увеличивать роль сдвига – например, загружение сосредоточенными силами вблизи от опор (на расстояниях порядка высоты поперечного сечения изгибаемого элемента) или несколькими близко расположенными друг к другу (на расстояниях того же порядка) примерно одинаковыми нагрузками, чередующимися по направлению. Конечно, в этих случаях речь идет о нагрузках, нормальных к осям элементов.

Таким образом, может оказаться необходимым учитывать в расчете деформации сдвига некоторого элемента конструкции, если выполняется одно или одновременно несколько следующих условий:

- сечение элемента – тонкостенное;

- материал – относительно низкомодульный при сдвиге (E/G > 3 ... 4);

- элемент достаточно «короткий, массивный» (h/l > 1/8);

- нагрузки таковы, что вызывают значительные поперечные силы при сравнительно небольших изгибающих моментах (ориентировочно: средние на грузовом участке |M/Q | ~ h).

Если суммарная длина элементов или их участков, где нужно учи-тывать сдвиг, составляет небольшую часть от общей длины всех элементов системы, то пренебрежение сдвигом может и не вносить существенных искажений в описание напряженно-деформированного состояния в частях конструкции, достаточно удаленных от зон со значительным влиянием сдвига, но в самих этих зонах погрешности определения усилий и, особенно, перемещений могут быть большими.

Для учета влияния сдвига в расчете статически неопределимой системы следует:

- при использовании метода сил вычисление коэффициентов и свободных членов канонических уравнений выполнять по формулам ( 8.69 ) или ( 8.70 ) с удержанием слагаемых, зависящих от поперечных сил (на участках, где это признано необходимым);

- при расчете методом перемещений применять для тех стержней, где нужно учитывать сдвиг, уточненные (с поправками на этот вид деформации) табличные данные для элементов основной системы метода перемещений – они даны в приложении 1.

8.12.2. Пример расчета плоской рамы с учетом деформаций сдвига стержней

Для рамы, изображенной на рис. 8.71, требуется построить эпюры внутренних силовых факторов по результатам расчетов с учетом и без учета деформаций сдвига горизонтальных и наклонных стержней.

Дано: l = 8 м , h = 6 м , q = 30 кН/м , F = 100 кН , E = 2×10⁵ МПа , n = 0,25 , I = 50000 см⁴ , A = 100 см², k_t = 5.

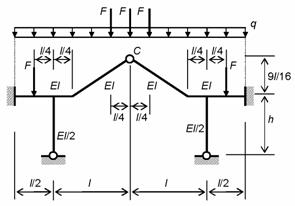
Рис.8.71

Решение:

Анализ расчетной схемы дает основание прогнозировать существенное влияние деформаций сдвига для рассматриваемой рамы из-за:

– наличия больших сосредоточенных нагрузок вблизи узлов;

– большого значения коэффициента k_t , свидетельствующего о том, что сечения ригелей – тонкостенные при достаточно большой относительной высоте горизонтальных стержней рамы (h_el / l_ell/8).

Ориентировочно высота тонкостенного двутавра может быть найдена по формуле

.

Система имеет одинаковые степени статической и кинематической неопределимости: n_st = n_k = 6. Трудоемкость расчета можно уменьшить, если учесть симметрию рамы и нагрузки. Будем рассматривать половину рамы слева от оси симметрии. Поскольку при симметричном деформировании верхний узел рамы не может смещаться по горизонтали (u_c = 0), то для компенсации влияния отбрасываемой правой половины в этом узле левой полурамы накладывается горизонтальная связь, обеспечивающая реализацию этого кинематического условия. Полученная таким образом расчетная модель половины рамы трижды статически и кинематически неопределима.

Наименьшее число основных неизвестных в ее расчете дает смешанный метод ( n = 2), основная система показана на рис. 8.72, канонические уравнения:

d₁₁ X₁ + d₁₂’Z₂ + D_1F = 0 ,

r₂₁’X₁ + r₂₂ Z₂ + R_2F = 0.

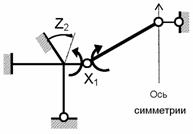
Рис.8.72

По методам сил и перемещений количества основных неизвестных одинаковые. В этом случае метод перемещений рациональнее, но из методических соображений расчет далее выполняется в двух вариантах – методами сил и перемещений. Решение смешанным методом не вносит ничего принципиально нового, поэтому не рассматривается.

Вариант А . Расчет рамы методом перемещений

Основная система для половины рамы представлена на рис. 8.73.

Канонические уравнения:

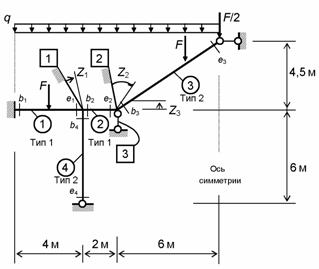
Рис.8.73

Вычисляем необходимые для расчета характеристики элементов основной системы:

– погонные жесткости при изгибе i_j = EI_j /l_j : i₁ = EI/(4м) = 3i , i₂ = EI/(2 м) = 6i , i₃ = EI/(7,5 м) = 1,6i , i₄ = (EI/2)/(6 м) = i ;

– относительные характеристики сдвига l_j = k_t,j (E_j/G_j)I_j /(A_jl_j²): так как сечения элементов 1, 2, 3 одинаковы, то для всех них k_t,j (E_j/G_j)I_j /A_j = 0,625 м² ( j =1, 2, 3), тогда l₁ = 0,625 м²/(4 м)² = 0,0391, l₂ = 0,625 м²/(2 м)² = 0,1562, l₃ = 0,625 м²/(7,5 м)² = 0,0111, l₄ = 0 (для 4-го элемента сдвиг не учитывается, то есть считается, что G₄ = ) .

C помощью таблиц приложения 1 строим эпюры изгибающих моментов в единичных состояниях основной системы (рис. 8.74) и определяем значения соответствующих поперечных сил Q_j,k (приведены под эпюрами M_k). Заметим, что поперечные силы в концевых сечениях в единичных состояниях Q_bj,k и Q_ej,k – одинаковые и равны Q_jk .

В скобках курсивом даны значения усилий, вычисленные без учета влияния сдвига – в предположении .

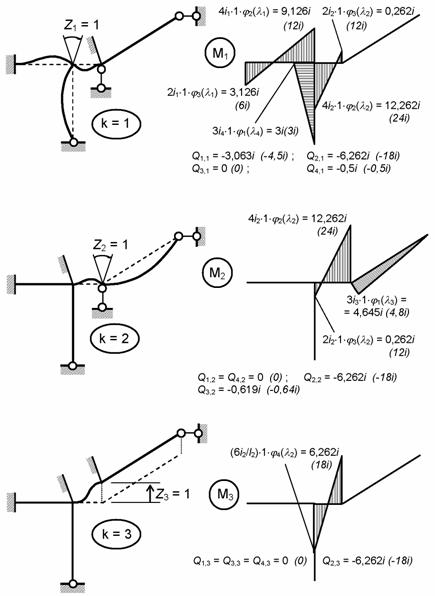
Рис.8.74

При определении ординат эпюр M_k использованы следующие значения множителей-функций, вносящих поправку на сдвиг:

j₁(l₃) = 1/(1+3l₃) = 0,9678; j₁(l₄) = 1; j₂(l₁) = (1+3l₁)/(1+12l₁) = 0,7605;

j₂(l₂) = (1+3l₂)/(1+12l₂) = 0,5109; j₃(l₁) = (1 – 6l₁)/(1+12l₁) = 0,5210;

j₃(l₂) = (1– 6l₂)/(1+12l₂) = 0,0218; j₄(l₂) = 1/(1+12l₂) = 0,3479 .

Рассматривая грузовое состояние основной системы (рис. 8.75), строим эпюры изгибающих моментов M_F и поперечных сил Q_F , при этом a₁(l₃) = j₁(l₃) = 0,9678.

Так как к элементу 3 приложены нагрузки, наклонные к его оси, в концевых сечениях b₃ и e₃ определяем также продольные силы, причем N_e3,F находим из условия равновесия Sy = 0 для узла С через нагрузку F/2 и известную поперечную силу Q_e3,F , а N_b3,F – из условия равновесия всего стержня 3:

N_e3,F = Q_e3,F ctga – (F/2) coseca = –211,92 кН (–210,64 кН) ;

N_b3,F = N_e3,F – (F + ql_x3)sina = –379,92 кН ( –378,64 кН) .

Заметим, что аналогично вычисляются отличные от нуля продольные силы в этом элементе во втором единичном состоянии N_b3,2 = N_e3,2 = –0,825i (–0,853i) .

Рис.8.75

Далее расчет выполняем в матричной форме с применением ЭВМ по следующей формуле для искомых усилий в концевых сечениях элементов:

S = S_F + S_oZ = S_F – S_o(a^тS_o)^-1(a^тS_F – c^тF_u) , ( 8.74 )

в которой для определения единичных реакций r используется вариант r = a^тS_o – через концевые усилия S_o в единичных состояниях.

Расчет на ЭВМ осуществляется дважды – с учетом и без учета влияния сдвига. В первом случае исходные матрицы таковы:

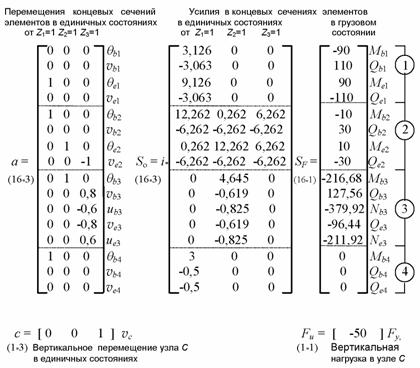
В случае пренебрежения влиянием сдвига исходные матрицы a , c и F_u остаются без изменений, а матрицы концевых усилий следующие:

Эпюры внутренних силовых факторов в раме для обоих случаев расчета представлены на рис. 8.76 (с учетом сдвига – сплошными линиями, без его учета – штриховыми).

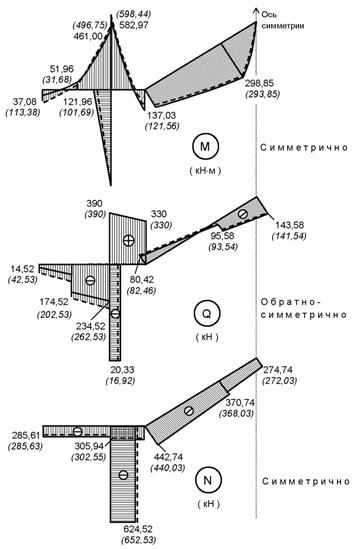
Рис.8.76

Анализ полученных результатов показывает, что вычисленное без учета деформации сдвига вертикальное перемещение узлов рамы на 28% меньше истинного, угол поворота узла соединения ригеля со стойкой – на 17%. Пренебрежение сдвигом приводит к завышению(!) наибольшего изгибающего момента в элементе 1 на 7,2%, в элементе 2 на 2,6% (для самого большого момента во всей конструкции) – эти ошибки не опасны, так как при подборе сечений по прочности они будут создавать некоторый излишний запас (конечно, не оправданный экономически). Погрешность вычисления наибольшего момента в наклонном стержне, для которого влияние сдвига изначально можно было ожидать меньшим, чем для 1-го и 2-го элементов (стержень 3 значительно длиннее при таком же, как у них, сечении), составляет 2,2%, но уже в сторону занижения. И наконец, «неожиданно» сильно заниженным – на 17% – оказывается изгибающий момент в стойке – стержне значительно более гибком, чем остальные (об этом можно судить по значениям погонных жесткостей i_j ) и, казалось бы, не вызывающем опасений по влиянию сдвига. Причиной тому дополнительная деформативность – за счет сдвига – смежных элементов (особенно 1-го), увеличивающая угол поворота узла (оценка Z₁ дана выше), что приводит к более сильному изгибу стойки. Несмотря на то, что моменты в ней значительно меньше, чем в ригелях рамы, но при меньшем (судя по исходным данным) сечении они могут оказаться опасными, и столь большая ошибка в их определении может иметь тяжелые последствия.

Вариант Б. Расчет рамы методом сил

Для трижды статически неопределимой половины рассматриваемой симметричной рамы основная система выбрана путем удаления трех угловых связей (рис. 8.77, а).

Схема нумерации ее расчетных участков и сечений приведена на рис. 8.77, б. Для участков 1 ... 6 учитывается деформация изгиба, а для участков 7 ... 11, геометрически совпадающих соответственно с 1... 5, – сдвиг. На участках 1... 5, где приложена распределенная нагрузка, назначено по три расчетных сечения (концевые b_j , e_j и посредине c_j ), на 6-м участке – два (b_j и e_j ), а для участков сдвига 7...11 – по одному c_j посредине.

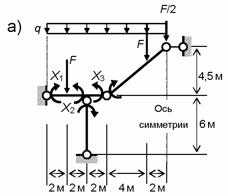
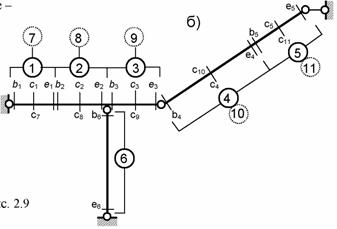
Рис.8.77

Канонические уравнения:

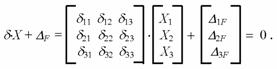
Вычисление усилий в расчетных сечениях выполняем с применением ЭВМ по матричной формуле

S = L_F + LX = L_F – L(L^тBL)^-1L^тBL_F ( 8.75 )

дважды – с учетом и без учета влияния сдвига.

Для формирования исходных матриц усилий в расчетных сечениях основной системы L (от единичных основных неизвестных) и L_F (от заданной нагрузки) рассматриваем единичные (рис. 8.78) и грузовое (рис. 8.79) состояния основной системы.

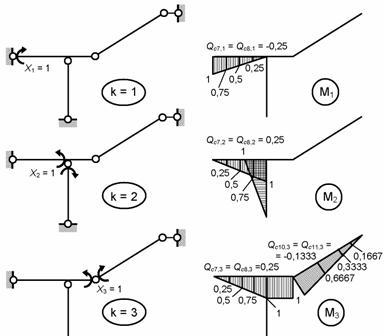
Рис.8.78

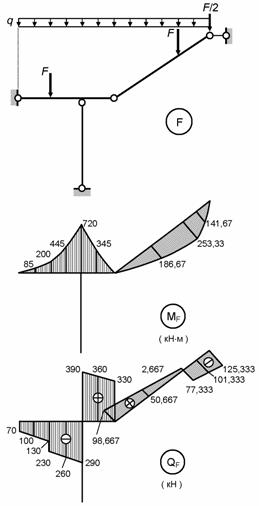
Рис.8.79

Построив эпюры M_k (k = 1, 2, 3), M_F , Q_F и вычислив в единичных состояниях поперечные силы Q_cj,k ( j = 7, 8,...,11; k = 1, 2, 3) в расчетных сечениях участков сдвига (их отличные от нуля значения приведены рядом с эпюрами M_k ), составляем матрицы L и L_F :

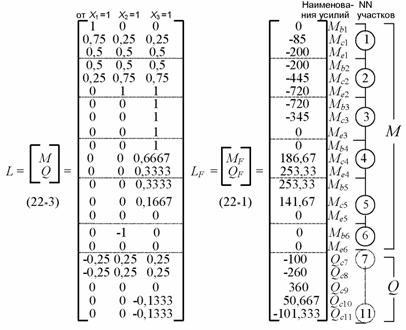
Матрица внутренней податливости основной системы B имеет следующую блочную структуру:

B = éB_M B_Q û = éB_M1 B_M2 ... B_M6 B_Q7 B_Q8... B_Q11 û .

Матрицы податливости участков при изгибе B_Mj ( j = 1,...,6) и при сдвиге B_Qj ( j = 1,...,11) могут формироваться «вручную» или автоматически в ходе расчета на ЭВМ – в последнем случае в исходных данных должны быть указаны длины и относительные жесткости сечений всех участков (с 1-го по 11-й). Для принятой расчетной схемы:

– длины участков: l₁ = l₂ = l₃ = l₇ = l₈ = l₉ = 2 м , l₄ = l₁₀ = 5 м , l₅ = l₁₁ = 2,5 м , l₆ = 6 м ;

– относительные жесткости c_j , выраженные через параметр С_о = EI (при изгибе c_j = EI_j /C_o , при сдвиге c_j = (GA_j /k_t,j)/C_o ): c₁ = c₂ = c₃ = c₄ = c₅ = EI/C_o = 1 , c₆ = (EI/2)/C_o = 0,5 , c₇ = c₈ = c₉ = c₁₀ = c₁₁ = 1,6 м^-2 (использованы заданные числовые значения A, I, k_t и n, при этом G/E = [2(1+n)]^-1 = 0,4 ).

Существуют и другие варианты формирования исходных матриц с учетом влияния сдвига – один из них описан в приложении 2.

Для расчета на ЭВМ без учета деформации сдвига в исходные данные вносятся изменения одним из следующих способов:

1) принимается G =, тогда c₇ = ... = c₁₁ =, но поскольку нельзя ввести в компьютер как число, то можно задать c₇ = ... = c₁₁ = 10⁴ ... 10⁵;

2) длины участков сдвига формально приравниваются нулю;

3) из исходных данных полностью исключается информация об участках сдвига.

В результате получены такие матрицы искомых усилий в расчетных сечениях:

Как и следовало ожидать, найденные значения изгибающих моментов в концевых сечениях элементов в трех первых значащих цифрах совпадают с вычислеными ранее методом перемещений в варианте А. Расхождения объясняются округлениями в исходных данных.

При построении эпюры поперечных сил концевые силы Q_bj и Q_ej на j-м участке сдвига можно определять с помощью приведенных в матрице S значений Q_cj:

Q_bj , Q_ej = Q_cj q_nj l_j /2 ,

где q_nj = q sin²b_j ( b_j – угол наклона оси j-го элемента к направлению нагрузки q ).

Продольные силы находятся из условий равновесия узлов.

Эпюры внутренних силовых факторов и анализ результатов расчета приведены ранее.

8.12.3. Оценка влияния продольных деформаций на усилия и перемещения в комбинированных системах

Деформации растяжения (сжатия) и соответствующие им напряжения и внутренние силовые факторы (продольные силы N) реально возникают во всех стержневых элементах конструкций. Но для некоторых из них этот вид деформации является главным (стержни ферм, тросовые и другие гибкие конструктивные элементы – ванты, затяжки и т.п.), а для других (колонн и ригелей рам, балочных частей комбинированных систем) – сопутствующим основной деформации изгиба.

Для элементов с преобладающим изгибом оценку влияния их продольной податливости на общие перемещения системы можно дать аналогично тому, как это было сделано для сдвига в п. 8.12.1:

, (8.76 )

где – относительная поправка за счет влияния растяжения (сжатия):

a_Q = D_iF,N /D_iF,M = h_sa_r²(h/l)^{2 ;} ( 8.77 )

h_s – коэффициент, учитывающий особенности системы и нагрузки, в частности, при постоянных и одинаковых на всех участках жесткостях сечений при изгибе EI и растяжении (сжатии) ЕА:

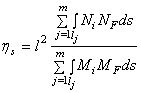(8.78)

Формулы ( 8.77 ) и ( 8.78 ) можно применить для оценки влияния продольных деформаций некоторого элемента системы. Если это стержень рамной конструкции, работающий преимущественно на изгиб, то продольные силы в нем того же порядка, что и поперечные силы (в этом можно убедиться, рассматривая равновесие узлов рамы). Тогда коэффициент будет близким по значению к коэффициенту , что видно из сравнения ( 8.78 ) и ( 8.71 ). Учитывая это, из сопоставления ( 8.76 ) и ( 8.72 ) можно заключить, что  меньше, чем , в 4 ... 10 раз в случае изотропного материала (нижняя граница относится к массив-ным сечениям типа прямоугольного, верхняя – к тонкостенным двутаврам).

Следовательно, для рам с достаточным основанием можно считать, что в общем вкладе, который вносит в некоторое перемещение конструкции своей деформацией сжато- или растянуто- изогнутый стержень, влияние его удлинений ( укорочений ) обычно почти на порядок меньше, чем деформации сдвига. В расчетах большинства рам этим влиянием можно пренебрегать.

К исключениям следует отнести многоэтажные рамы и случаи действия нагрузок вдоль осей стержней (или с небольшими эксцентриситетами).

В комбинированных системах учет продольной податливости элементов рамно-балочных частей может стать необходимым, если примыкающие к ним затяжки, ванты, шпренгели и т.п. наклонены к их осям под небольшими углами (меньше 20 ... 25^о).

Для арок как конструкций, в значительной мере воспринимающих нагрузки за счет работы на сжатие, характерно более высокое, чем в рамах, влияние обжатия оси – это уже отмечалось выше в п.6.2. Продольные силы в арках обычно в несколько раз, а часто – на порядок и более – превосходят поперечные силы (речь идет о сопоставлении средних интегральных абсолютных величин), даже если арка не является близкой к безмоментной. В последнем случае влияние продольных деформаций, связанных с силами N, становится определяющим.

Пренебрегать обжатием оси допустимо лишь для достаточно высоких (так называемых подъемистых) арок со стрелами подъема более 1/6 ... 1/5 пролета, и то лишь при существенно асимметричных нагрузках.

В отличие от сжато- или растянуто-изогнутых стержней, конструктивные элементы, предназначенные для работы практически чисто на растяжение (сжатие), – такие, как затяжки, шпренгели, ванты, оттяжки, стойки и т.п., своими продольными деформациями в подавляющем большинстве случаев сильно влияют на распределение усилий и перемещений в статически неопределимых системах.

Это объясняется тем, что при том же порядке значений продольных сил, как и в соседних рамно-балочных элементах, эти стержни имеют значительно меньшие поперечные сечения, вследствие чего их абсолютные удлинения (укорочения) могут оказаться соизмеримыми с перемещениями, возникающими от изгиба других элементов. Поскольку обычно для растянутого элемента сечение подбирают из условия прочности (R – расчетное сопротивление материала), то удлинение стержня в расчетном состоянии будет, по закону Гука, ( l – длина). Очевидно, что чем длиннее растянутый элемент, тем сильнее его деформация влияет на перемещения (а в статически неопределимых системах – и на усилия) в конструкции. Рекомендуется обратить внимание на то, что применение более прочного материала (с увеличенным расчетным сопротивлением R) приведет к увеличению деформаций и перемещений, так как модуль упругости Е мало изменяется даже при существенном варьировании прочностных характеристик таких материалов, как строительные стали и др. Имеет значение и то, как располагается продольно деформируемый элемент в системе с кинематической точки зрения.

Например, для комбинированной системы, изображенной на рис. 8.80, воздействие наклонного растянутого стержня на перемещения, изгибающие моменты и поперечные силы в балке принципиально аналогично тому, которое оказывает упругая опора в примере, показанном на рис. 8.70, но дополнительно в левой части балки возникает продольная сила N_BC = –N_CH cos.

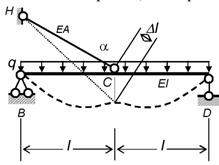
Рис.8.80

Перемещение середины балки по вертикали , или, выразив через R , E и l_CH = l_BC /cos , получаем v_c = 2Rl /(Esin2).

При = 45^о v_c = 2RL / E , а при =15^о – вдвое больше. Отсюда ясно, что в подобных ситуациях и для других видов комбинированных систем удлинения (укорочения) такого типа элементов при малых углах их наклона могут сказываться достаточно сильно.

8.12.4. Примеры расчета комбинированной системы с учетом продольных деформаций стержней

Пример 1.

Выполнить расчеты комбинированной системы, изображенной на рис. 8.81, построить эпюры внутренних силовых факторов и дать анализ полученных результатов с учетом и без учета продольных деформаций безызгибно работающих элементов.

Дано: l = 12 м , h = 8 м , q = 40 кН/м , E = 2∙10⁵ МПа , I = 10⁵ см⁴ , А = 20 см².

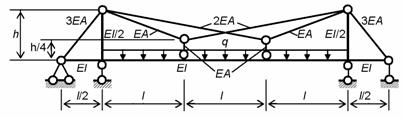
Рис.8.81

Система 6 раз статически неопределима. Степень кинематической неопределимости равна 12, если учитываются удлинения стержней, работающих только на растяжение (сжатие), и уменьшается до 4 , если продольными деформациями этих стержней пренебрегать. Во всех случаях балку и пилоны считаем продольно недеформируемыми.

Если принять во внимание симметрию системы и нагрузки и использовать группировку основных неизвестных, то число симметричных неизвестных по методу сил составит 3, а по методу перемещений – 6 и 2 соответственно с учетом и без учета продольных деформаций стержней. Таким образом, рациональным для расчета заданной системы является метод сил, даже несмотря на то, что в одном варианте метод перемещений дает меньше неизвестных (всего 2) – это не компенсирует дополнительной работы по выполнению расчета, совершенно независимого от того, что делается в другом варианте (с учетом ), где метод сил безусловно выгоднее.

Основная система метода сил с только симметричными (ненулевыми) групповыми основными неизвестными показана на рис. 8.82.

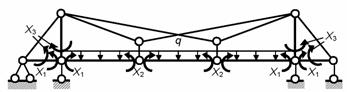
Рис.8.82

Для такого типа конструкций за основные неизвестные иногда принимают усилия в поддерживающих балку вантах, подвесках и оттяжках. В этом случае основная система получается принципиально отличной по своей работе от заданной, вследствие чего в исходных данных (эпюрах и матрицах) возникают большие числа, ухудшается обусловленность системы уравнений, страдает точность расчета. Поэтому настоятельно не рекомендуется применять такие основные системы.

Рассматриваем единичные (рис. 8.83) и грузовое (рис. 8.84) состояния основной системы. Построение эпюр изгибающих моментов не составляет труда. Продольные силы в стержнях, для которых предполагается учитывать деформации растяжения (сжатия), находятся из условий равновесия узлов. В 1-м и 2-м единичных состояниях продольные силы отличаются только знаками. Значения продольных сил проставлены рядом с соответствующими стержнями на схеме.

Для вычисления искомых усилий в заданной статически неопределимой системе по матричной формуле ( 8.58 ) используем ЭВМ. Исходные матрицы можно составлять лишь для половины системы (по одну сторону от оси симметрии). Схема нумерации расчетных участков и сечений дана на рис. 8.85. На 2-м и 3-м участках, где на балку действует распределенная нагрузка q , назначены по три расчетных сечения – концевые b_j, e_j и cреднее c_j. На 1-м и 3-м участках, где эпюры изгибающих моментов во всех состояниях основной системы линейные, расчетные сечения – только концевые b_j и e_j . На участках 5, 6, ... , 9 стержней, испытывающих только равномерное осевое растяжение (сжатие) взято по одному сечению c_j .

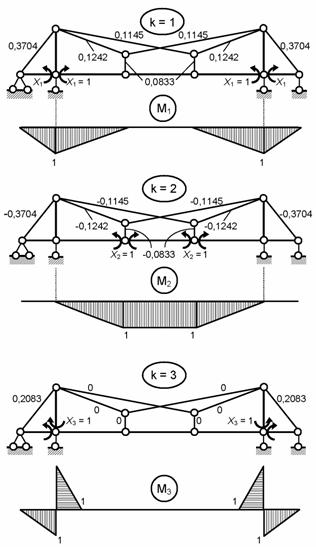
Рис.8.83

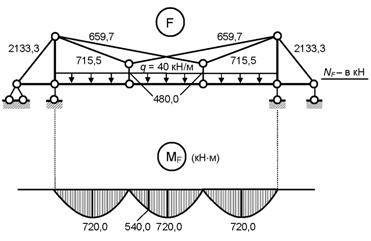
Рис.8.84

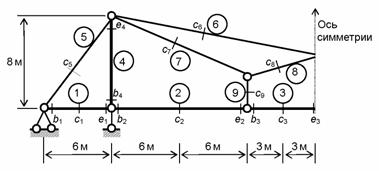
Рис.8.85

Матрицы усилий в расчетных сечениях основной системы L (в единичных состояниях) и L_F (в грузовом состоянии):

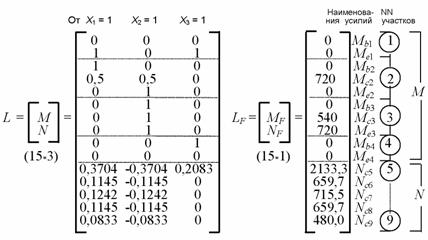
Матрица внутренней податливости В основной системы состоит из матриц податливости расчетных участков при изгибе и растяжении (сжатии): B = éB_M B_N û = éB_M1 B_M2 B_M3 B_M4 B_N5 B_N6 B_N7 B_N8 B_N9 û. 

Приведем примеры формирования некоторых блоков:

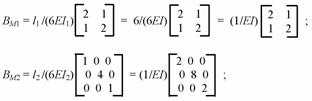
B_N5 = [l₅ /EA₅] = [10/(3EA)] = (1/EI )[10×EI /(3EA)] = (1/EI )[3,333×I /A] = (1/EI)[1,6667] – здесь учтено, что l₅ = 10 м и I /A = 10⁵ см⁴/(20 см²) = 5000 см² = 0,5 м².

Возможно автоматическое формирование матрицы В – для этого в компьютер вводятся сведения о расчетных участках:

– длины l₁ = 6 м ; l₂ = 12 м ; l₃ = 6 м ; l₄ = 8 м ; l₅ = 10 м ; l₆ = 18,55 м ; l₇ = 13,42 м ; l₈ = 6,18 м ; l₉ = 2 м ;

– относительные (выраженные через параметр C_o = EI ) жесткости сечений c_j = EI_j /C_o ( j = 1,..., 4); c_j = EA_j /C_o ( j = 5,…, 9):

c₁ = c₂ = c₃ = 1; c₄ = 0,5; c₅ = 6 м^-2; c₆ = c₈ = 4 м^-2; c₇ = c₉ = 2 м^-2.

Расчет конструкции на ЭВМ выполняем дважды – с учетом и без учета продольных деформаций элементов 5 ... 9. В первом случае используются сформированные выше исходные данные, а во втором в них вносятся изменения, которые приведут к исключению влияния податливости стержней при растяжении (сжатии). Это можно сделать одним из следующих способов:

1) жесткости ЕА_j полагаются бесконечно большими, тогда c₅ =...= c₉ = (реально в ЭВМ вводят не бесконечные, но большие значения c₅ ... c₉ – порядка 10⁴... 10⁵, от этого может возникать погрешность в 5-й – 6-й значащих цифрах результатов);

2) длины стержней 5 ... 9 условно задают равными нулю;

3) из исходных данных вообще исключаются все сведения, относящиеся к элементам 5 ... 9 (при этом нужно иметь в виду то, что в результате не будут вычислены продольные силы в этих стержнях).

По компьютерной распечатке получены матрицы искомых усилий – моментов и продольных сил в расчетных сечениях конструкции:

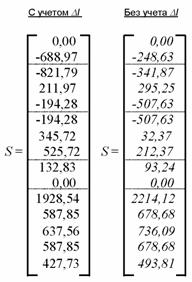
Эпюры внутренних силовых факторов в балке и пилоне (для половины системы) представлены на рис. 8.86. Поперечные силы в концевых сечениях участков вычислены по изгибающим моментам обычным приемом:

Q_bj , Q_ej = ( M_ej – M_bj )/l_j q_jl_j /2 .

Продольные силы в балке и пилоне найдены из условий равновесия узлов. Сплошными линиями и прямыми цифрами даны эпюры и значения их ординат, полученные расчетом, в котором учтены удлинения элементов, а штриховыми линиями и курсивом в скобках – без учета .

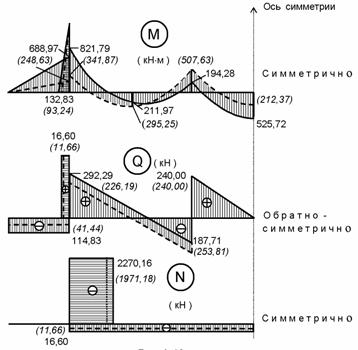
Рис.8.86

Сравнительный анализ результатов, полученных в двух вариантах расчета, показывает:

1) найденные с учетом продольной податливости растянутых стержней и, следовательно, более точные значения продольных сил в оттяжке (элемент 5) на 12,9%, а в вантах 6, 7, 8 и подвеске 9 – на 13,4% меньше, чем при расчете в пренебрежении удлинениями этих стержней;

2) значения изгибающих моментов в характерных сечениях конструкции, найденные без учета продольных деформаций элементов, в несколько раз (!) отличаются от выявленных более точным расчетом – на крайнем участке балки они занижены в 2,77 раза, в пилоне – в 1,42 раза, в сечениях b₂ и e₃ – соответственно в 2,40 и 2,48 раза, а в сече-ниях e₂ и b₃ – в 2,61 раза, но уже в сторону завышения;

3) распределение моментов, полученное упрощенным (без учета ) расчетом, существенно отклоняется от действительного как по общей картине – более «равномерной» по средним абсолютным величинам, так и по интервалу значений (от –507,63 до +297,63 кНм в точке максимума между сечениями b₂ и c₂, в то время как по более точному расчету – от –821,79 до +525,72 кНм);

4) расположение опасных сечений по двум вариантам расчета прин-ципиально разное: при учете сечение балки с M_max оказывается на оси симметрии конструкции, а с M_min – в начале 2-го участка (справа от узла примыкания пилона); без учета опасное по M_max сечение получается вблизи середины 2-го участка, а по M_min – в месте прикрепления под-вески.

Общий вывод: упрощенный расчет, в котором работающие на чистое растяжение стержни считаются недеформируемыми (жесткими), лишь для продольных сил в этих стержнях дает ошибку «в запас прочности» (завышая значения N). Ошибки в определении изгибающих моментов настолько велики, что такой подход недопустим даже на стадии предварительной оценки усилий в комбинированных системах рассмотренного типа или подобных им.

Пример 2.

Рассчитать раму (рис. 8.87) с учетом и без учета деформаций затяжки и подкосов, построить эпюры внутренних силовых факторов и выполнить сравнительный анализ результатов двух расчетов.

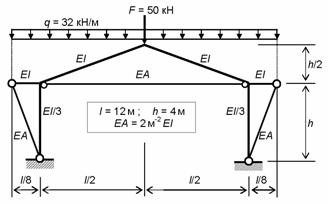
Рис.8.87

Сведения о степенях статической и кинематической неопределимости системы и о числе симметричных и обратно-симметричных неизвестных в разных вариантах расчета методами сил и перемещений приведены в таблице.

Вариант расчета	Степень неопределимости		Число основных неизвестных
			Метод сил		Метод перемещений
			Симм.	Обр.симм.	Симм.	Обр. симм.
С учетом	4	7	3	1	3	4
Без учета		4			1	3

К рассматриваемому случаю симметричного загружения рамы относятся данные, выделенные жирным курсивом. Из их сравнения следует, что рациональным в данной задаче является метод перемещений.

Используя для уменьшения трудоемкости расчета симметрию конструкции и нагрузки, рассматриваем левую от оси симметрии половину рамы. Влияние на нее отбрасываемой правой половины моделируем наложением связей, обеспечивающих для половины рамы выполнение таких же кинематических условий по перемещениям сечений, расположенных на оси симметрии, как и во всей конструкции. Верхний узел и среднее сечение затяжки при симметричной деформации всей системы не поворачиваются ( = 0 ) и не смещаются по горизонтали ( u = 0 ) – этим условиям отвечает подвижное по вертикали защемление – именно его и вводим в верхний узел полурамы. Что касается затяжки, то поскольку она, по своей природе, не работает на изгиб, то защемление для нее является излишним – можно было бы ограничиться наложением на правом конце половины затяжки лишь горизонтальной линейной связи, обеспечивающей u = 0. Но поскольку при этом формально возникает мгновенная изменяемость, условно добавляем и вертикальную линейную связь (она не будет включаться в работу!), в результате чего получаем цилиндрический шарнир. Сформировав таким образом эквивалентную расчетную схему половины рамы (она трижды кинематически неопределима), выбираем для нее основную систему метода перемещений (рис. 8.88).

На схеме обозначены номера наложенных на узлы связей (в квадратах) и соответствующие им основные неизвестные Z₁ , Z₂ и Z₃, номера узлов (в треугольниках) и элементов (в кружках) с указанием их типов по принятой классификации. На каждом изгибаемом элементе отмечены его концевые сечения b_j и e_j ( j = 1, 2, 3) (для элементов 2-го типа b_j назначается у защемленного конца), а на стержнях 4 и 5, работающих на осевое растяжение (сжатие) – произвольное сечение с_j .

Длины элементов: l₁ = 1,5 м ; l₂ = 6,325 м ; l₃ = 4 м ; l₄ = 4,272 м ; l₅ = 6 м ; погонные жесткости при изгибе i_j = EI_j /l_j ( j = 1, 2, 3): i₁ = EI /(1,5 м) = 8i ; i₂ = EI /(6,325 м) = 1,9i ; i₃ = (EI /3)/(4 м) = i .

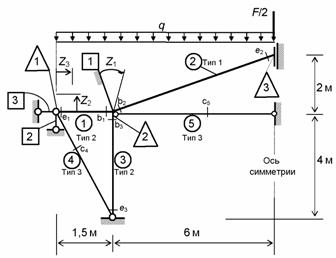
Рис. 8.88

Рассматриваем единичные состояния основной системы (рис. 8.89). С помощью таблиц метода перемещений строим эпюры изгибающих моментов M_k ( k = 1, 2, 3) и определяем постоянные по длине участков 1, 2, 3 поперечные силы Q_j,k (их значения приведены рядом с эпюрами M_k ). Также с помощью табличных данных строятся эпюры изгибающих моментов и находятся поперечные силы в основной системе от заданной нагрузки (рис. 8.90).

Для выполнения расчета в дальнейшем понадобятся продольные силы в элементах 4 и 5, удлинения (укорочения) которых нужно учитывать, и в стержне 2, нагруженном наклонно к его оси. Продольные силы в затяжке и подкосе определяем по закону Гука: N_j,k = EA_j ×Dl_j / l_j ( j = 4, 5; k = 1, 2, 3). Из схем деформаций основной системы в единичных состояниях (см. рис. 8.89) видно, что подкос удлиняется во 2-м состоянии ( = 0,9363) и укорачивается в 3-м (= – 0,3511), а затяжка получает укорочение лишь при Z₃ = 1 ( = – 1), поэтому N_4,1 = N_5,1 = N_5,2 = 0; N_4,2 = EA₄×Dl_4,2 / l₄ = 2 м^-2 EI×0,9363/(4,272 м) = 0,4383EI = 5,26i ;

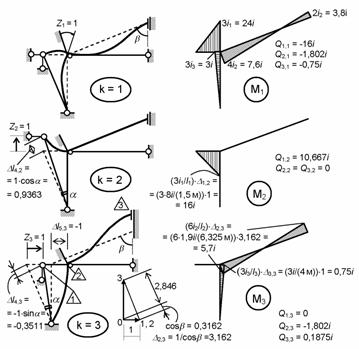
Рис.8.89

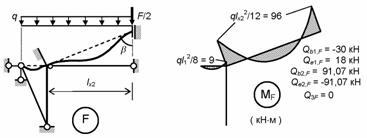
Рис.8.90

N_4,3 = EA₄×Dl_4,3 / l₄ = 2 м^-2 EI (– 0,3511)/(4,272 м) = – 0,1644EI = – 1,972i ;

N_5,2 = EA₅×Dl_5,2 / l₅ = 2 м^-2 EI (– 1)/(6 м) = – EI/3 = – 4i.

В грузовом состоянии (см. рис. 8.90) стержни 4 и 5 не деформируются, вследствие чего N_4,F = N_5,F = 0.

Продольные силы в концевых сечениях e₂ и b₂ наклонного стержня определяются из условий равновесия узла 3 и всего элемента 2. В грузовом состоянии: N_e2,F = – (F/2+Q_e2,F sinb)/cosb = – 352,27 кН; N_b2,F = N_e2,F – – ql_x2×cosb = – 412,98 кН. В единичных состояниях: N_e2,k = N_b2,k = – Q_2,k tgb; откуда N_e2,1 = N_b2,1 = – 5,406i ; N_e2,2 = N_b2,2 = 0 ; N_e2,3 = N_b2,3 = – 5,406i.

Для вычисления на ЭВМ искомых усилий по формуле ( 8.74 ) формируем исходные матрицы:

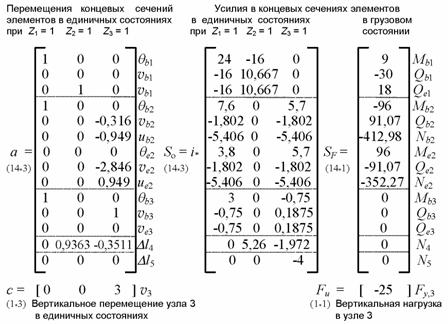
Если выполнять расчет без учета продольной податливости элементов 4 и 5, то степень линейной подвижности узлов становится равной нулю, и симметричное основное неизвестное будет одно – угол поворота Z₁. Основная система может быть получена как частный случай изображенной на рис. 8.88 исключением из нее линейных связей 2 и 3 .

Схемы деформаций в единственном единичном состоянии (при Z₁ = 1) и в грузовом состоянии остаются такими же, как показано на рис. 8.89 и 8.90, при этом не изменяются изгибающие моменты и поперечные силы, а также продольные силы в наклонном стержне. Но продольные силы в затяжке и подкосе следует определять иначе, чем в расчете с учетом их продольных деформаций, так как попытка применить закон Гука дает для усилий N_4,k и N_5,k неопределенности вида 0× (жесткости ЕА₄ и ЕА₅ считаются бесконечными, а деформации и – нулевые). Используя условия равновесия узлов 1 и 2 в единичном состоянии, получаем: N_4,1 = – Q_e1,1 /cosa = 17,089i ; N_5,1 = – N_2,1 sinb – Q_b2,1 cosb + Q_b3,1 – N_4,1sina = – 1,052i.

По таким же формулам (заменяя индекс состояния 1 на F), находим N_4,F = – 19,22 кН; N_5,F = 369,70 кН – от заданной нагрузки.

Исходные матрицы a , S_o и c в этом варианте расчета имеют лишь по одному столбцу, причем a и c совпадают с первым столбцом одноименных матриц, составленных для расчета с учетом , а матрица S_o получается из первого столбца аналогичной ранее составленной матрицы путем замены нулей в последних двух позициях на только что найденные значения N_4,1 и N_5,1 . Матрица S_F также изменяется – в двух последних позициях вместо нулей вписываются N_4,F и N_5,F. Матрица F_u не изменяется.

В результате двух расчетов на ЭВМ получены следующие матрицы основных неизвестных Z и искомых усилий:

Эпюры внутренних силовых факторов в левой половине заданной рамы показаны на рис. 8.91 (сплошными линиями – с учетом продольных деформаций стержней 4 и 5, штриховыми – без них). Соответствующие ординаты даны прямым шрифтом и курсивом в скобках.

На участках 1, 3, 4 и 5, где продольные силы постоянные, проставлены лишь их значения, без изображения эпюр.

Сравнение результатов, полученных в двух вариантах расчетов, показывает:

1) изгибающие моменты, вычисленные упрощенным способом – без учета удлинений подкоса 4 и затяжки 5, получились заниженными по сравнению с найденными более точным расчетом – в 2,56 раза на 1-м участке, в 7,86 (!) раза в стойке рамы, в наклонном ригеле по максимальным (положительным) моментам – в 1,84 раза, по минимальным (наибольшим отрицательным) – в 2,24 раза; при этом обращает на себя внимание то, что опасные по M_max и M_min сечения 2-го стержня в двух вариантах расчета располагаются совершенно по-разному: более отвечающие действительности M_max и M_min, найденные с учетом деформаций растянутых стержней 4 и 5, возникают соответственно на расстоянии 1,41 м от верхнего (конькового) узла рамы и на левом конце ригеля, а при упрощенном расчете – на расстоянии 3,0 м от узла 2, то есть примерно посередине ригеля, и на правом его конце;

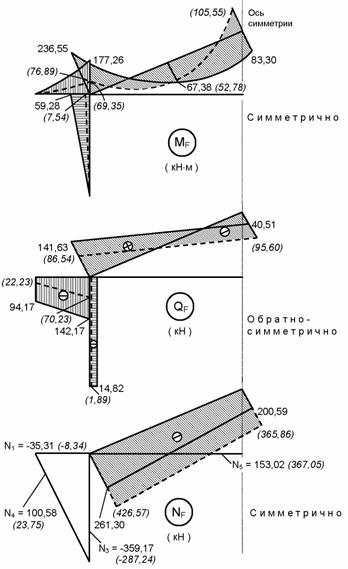
Рис.8.91

2) общее распределение изгибающих моментов, получающееся в пренебрежении продольной податливостью затяжки и подкоса, – более «равномерное» в среднем по абсолютным величинам и с существенно меньшими расчетными значениями M_max и M_min, чем в действительности, что создает искаженное представление о работе конструкции и неизбежно приведет к грубым ошибкам в оценке ее прочности;

3) угол поворота узла 1 (основное неизвестное Z₁) по упрощенному расчету также получается значительно (в 4,06 раза) меньше найденного по более точному варианту, следовательно, и перемещения в системе сильно занижаются, то есть конструкция необоснованно может быть оценена как существенно более жесткая, чем на самом деле;

4) продольные силы, вычисленные без учета продольных деформаций элементов 4 и 5, меньше, чем в случае учета этих деформаций, в стержнях 1 и 4 в 4,23 раза, в стойке 3 – в 1,25 раза, и лишь в затяжке и наклонном ригеле они завышаются соответственно в 2,40 и 1,72 (в среднем) раза.

Общий вывод: расчет рамы с затяжкой и подкосами, работающими на чистое растяжение, в котором игнорируются деформации этих стержней, дает очень сильно ( в несколько раз ! ) заниженные перемещения и расчетные изгибающие моменты. Поэтому он недопустим даже на стадии предварительной оценки усилий и перемещений в конструкциях подобного типа.

8.12.5. Учет изгиба стержней ферм

В предыдущих разделах рассматривались стержневые конструкции, для которых изгиб является основным видом деформации значительной части элементов. Но в некоторых случаях, например, для арок при определенных условиях загружения , изгиб может оказаться деформацией, лишь сопровождающей сжатие.

Конструкциями, изгиб стержневых элементов которых в большинстве расчетов, как правило, никак не учитывается, являются фермы. Такой подход основывается на представлении о работе фермы как идеализированной системы со строго прямолинейными стержнями, осевые линии которых пересекаются точно в центрах узлов, причем соединения элементов – идеальные шарнирные (без трения), а нагрузки - сосредоточенные силы в узлах.

В действительности:

- узлы ферм не бывают шарнирными (соединения стержней, в зависимости от конструктивного решения, представляют собой упругие или неупругие защемления – в большей или меньшей степени податливые в деревянных, сборных железобетонных и стальных бесфасоночных фермах, либо почти жесткие в металлических сварных фермах с фасонками и в монолитных железобетонных фермах);

- возможна «расцентровка» осей стержней в узлах;

- стержни фермы могут иметь начальные искривления (погиби);

- нагрузки могут быть приложены с эксцентриситетами относительно центров узлов.

Следствием вышеуказанных обстоятельств является возникновение изгиба стержней фермы. Оценить влияние каждого из перечисленных факторов можно на примере фермы, рассмотренной в учебнике [ 1 ], где на c. 15–16 даны результаты расчета на действие нагрузки, показанной на рис. 8.92, в предположении абсолютно жесткого соединения стержней в узлах (этот случай является самым неблагоприятным – изгибающие моменты получаются наибольшими при прочих равных условиях).

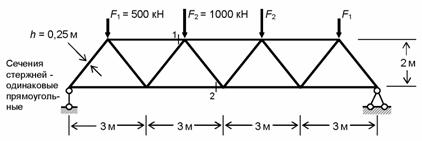
Рис.8.92

А) Данные, представленные на рис. 1.13 в [ 1 ], свидетельствуют о том, что продольные силы в системе c жесткими узлами меньше, чем вычисленные по традиционной шарнирной схеме, причем разница не превышает 1% для поясов фермы и 2,1% для раскосов. Соответствующие изгибающие моменты имеют значения, указанные без скобок на рис. 6.28.

Расчет фермы как статически неопределимой системы с жесткими узлами выполнен в [ 1 ] методом перемещений. При этом рассмотрена половина симметричной конструкции со степенью кинематической неопределимости расчетной схемы = 13. Степень статической неопределимости той же половины фермы = 11, следовательно, можно применить для расчета и метод сил. Основную систему в этом случае целесообразно выбрать в виде фермы с шарнирными узлами.

Наибольший момент, равный 29,5 кНм, возникает в сечении 1 (рис. 8.91) стержня, продольная сила в котором –1859,2 кН (при расчете по шарнирной схеме –1875 кН). Если принять ширину сечения b = h/2 = 12,5 см, то фибровые напряжения от изгиба и сжатия получаются равными соответственно 22,7 МПа и 59,5 МПа. В сечении 2 стержня нижнего пояса с наибольшей продольной силой 2599,8 кН (в ферме с шарнирными узлами – 2625 кН) изгибающий момент равен 22,4 кНм. Он вызывает фибровое напряжение 17,3 МПа (от продольной силы – 83,2 МПа). При этом полное напряжение получается на 21% больше, чем вычисленное по шарнирной схеме, и, следовательно, в рассмотренном случае пренебрегать изгибом стержней фермы нельзя.

Рис.8.93 Рис.8.94

Анализируя приведенные выше данные, нужно иметь в виду то, что они получены при следующих условиях:

а) ферма рассчитана как линейно деформируемая система (то есть по недеформированной схеме, без учета явления продольно-поперечного изгиба элементов);

б) стержни фермы достаточно массивные (жесткие) - высота сечений всех элементов h = 0,25 м составляет 1/10 ... 1/12 их длины.

Б) Расчет по деформированной схеме (с учетом конструктивной нелинейности) для систем, стержни которых испытывают интенсивное растяжение или сжатие, будет давать другие значения изгибающих моментов – для рассматриваемой фермы эпюра показана на рис. 8.94 (при Е = 3×10⁴ МПа). Обращает на себя внимание то, что моменты в растянутых стержнях в среднем больше, чем вычисленные без учета эффекта продольно-поперечного изгиба, а в сжатых – меньше. Так, в сечении 1 уточненное значение момента получилось меньше в 1,4 раза, а в сечении 2 – в 1,65 раза больше. Объяснить это можно тем, что растянутые элементы при работе на изгиб проявляют себя как более жесткие, чем сжатые, и вследствие этого в большей степени участвуют в восприятии изгиба. Заметим, что уточнения в значениях продольных сил при этом не превышают 0,1%. Наибольшее нормальное напряжение – оно возникает в сечении 2 – становится уже на 33% больше, чем найденное расчетом по шарнирной схеме.

В) Оценивая влияние такого фактора, как гибкость стержней, следует отметить, что увеличение гибкости (оно сопровождается также увеличением отношения EА / EI жесткостей сечений элементов при растяжении-сжатии и изгибе) при расчете по недеформированной схеме приводит к уменьшению изгибающих моментов.

Например, если изменить размеры сечений всех стержней фермы в сравнении с принятыми выше, так чтобы гибкость элементов поясов фермы примерно удвоилась и стала бы равной 80, то отношение ЕА / ЕI возрастет в 3,65 раза, а изгибающие моменты уменьшатся в среднем в 3,6 раза (их значения даны в скобках на рис. 8.93).

Но более точный расчет – по деформированной схеме – показывает, что в наиболее напряженных сжато-изогнутых элементах увеличение гибкости может вызывать увеличение изгибающих моментов, причем тем большее, чем ближе значения продольных сил к критическим.

Таким образом, пренебрежение изгибом стержней может быть опасным с точки зрения оценки прочности конструкции, особенно для ферм с «жесткими» (массивными) стержнями. Вычислять изгибающие моменты в них следует, как правило, с учетом эффекта продольно-поперечного изгиба.

Далее рассмотрим такие факторы, как несовершенства геометрии фермы и неузловое приложение нагрузок.

Г) Эксцентричное примыкание стержня к узлу. В качестве примера возьмем средний стержень верхнего пояса фермы (в нем действует наибольшая сжимающая продольная сила) с одинаковыми смещениями его концов от центров узлов вверх на е_о (рис. 8.95, а). Эксцентричность прикрепления концов стержня к узлам моделируется бесконечно жесткими вставками и учитывается при описании геометрии расчетной схемы. Рассчитав ферму (по недеформированной схеме) как симметричную систему с жесткими узлами при тех же нагрузках и размерах, что на рис. 8.92, для е_о = 1 см находим изгибающие моменты, эпюра которых приведена на рис. 8.95, б сплошными линиями. Там же штриховыми линиями с ординатами в скобках даны моменты для случая такого же отклонения е_о = 1см в противоположную сторону (вниз).

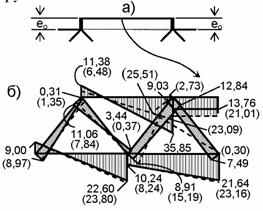
Рис.8.95

Д) Влияние начальных геометрических несовершенств ( погибей ) стержней оценим, рассматривая простейшее по форме – в виде треугольника – начальное отклонение от проектной прямолинейной оси среднего стержня верхнего пояса (рис. 8.96, а). Приняв верхнюю точку треугольника за дополнительный узел расчетной схемы с ординатой, учитывающей величину f_o , в результате расчета при f_o = d /100 = 3 см и таких же прочих исходных данных, как на рис. 8.92, получаем эпюры моментов (рис. 8.96) для двух случаев – f_o вверх (сплошные линии) и f_o вниз (штриховые линии с ординатами в скобках).

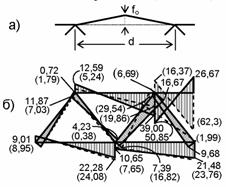
Рис.8.96

Е) Изгиб от нагрузок, приложенных со смещениями относительно центров узлов, удобно изучать, заменяя их эквивалентными узловыми воздействиями. Для одиночной сосредоточенной силы на некотором стержне фермы (рис. 8.97, а) указанная замена дает загружение, представленное на рис. 8.97, б, где F_l = F× v[1+ u(v – u)]; F_r = F× u[1+v(u – v)] = F – F_l ; M_l = Fd× uv² ; M_r = Fd× u²v.

Эквивалентные силы и моменты суммируются с заданными узловыми нагрузками. Далее расчет на суммарные силы в узлах выполняется обычным порядком, и влияние вызываемого ими изгиба оценивается так, как это сделано выше.

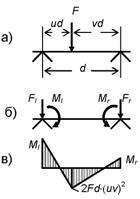
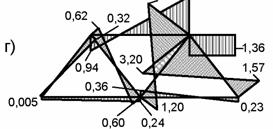
Рис.8.97

На действие узловых моментов ферма рассчитывается отдельно. Например, при симметричном смещении нагрузок F₂ (рис. 8.92) на e_F = 1 см от центров узлов имеем F_l = F_r = F₂; M_l = M_r = F₂ e_F = 10 кНм. Эпюра изгибающих моментов от одновременно приложенных M_l и M_r показана на рис. 8.97, г.

Полные изгибающие моменты в стержне, к которому приложена неузловая нагрузка, получаются суммированием результатов расчета на действие эквивалентных узловых воздействий и «локальных» моментов с эпюрой по рис. 6.32, в.

Сравнение эпюр, приведенных на рис. 8.93, 8.95 и 8.96, а также анализ данных рис.8.97, г показывают, что распределение изгибающих моментов, вызванных геометрическими несовершенствами e_o , f_o и внешними моментами в узлах, носит локальный характер, с достаточно быстрым затуханием по мере удаления от места реализации любого из указанных факторов.

---

email: KarimovI@rambler.ru

Адрес: Россия, 450071, г.Уфа, почтовый ящик 21

Теоретическая механика Сопротивление материалов

Прикладная механика Детали машин Теория машин и механизмов

00:00:00