Главная
9.7.7.
Конечно-элементная формулировка плоской задачи теории упругости: базовые
соотношения
9.7.7.1.
Ослабленная формулировка задачи теории упругости
Задачи математической физики могут быть поставлены различным образом. Принято различать три основные формулировки краевых задач математической физики и в частности задачи теории упругости:
1. Прямая (строгая) формулировка, представляющая собой исходную систему дифференциальных уравнений;
2. Ослабленная формулировка, выражаемая в виде некоторого вариационного принципа;
3. Обратная формулировка, в которой исходное уравнение задачи выражено в виде некоторого интегрального уравнения.
Диаграмма Тонти представленная
в прошлой лекции на рис. 9.52 представляла собой прямую формулировку задач
теории упругости. Все соотношения между физическими переменными в данном случае
должны выполняться в каждой точке тела. Это строгое условие схематично выражено
черными линиями на диаграмме (рис. 9.52).
Ослабленная формулировка изображена на рис. 9.54.
Схематично она может быть получена путем ослабления одного или более строгого
соотношения. На рис. 9.54 такие ослабленные соотношения изображены серыми
линиями. Ослабленные соотношения означают, что соответствующие уравнения
выполняются не в каждой точке тела, а в среднем, т.е. в некотором интегральном
смысле. Ослабленные связи обеспечиваются с помощью некоторых вариационных
формулировок, подходящих для данной задачи. Заметим, что, в общем, для одной и
той же задачи может быть сформулирован не один вариационный принцип, и,
следовательно, может быть составлено множество ослабленных формулировок задачи.
В противоположность этому прямая, или строгая, формулировка всегда единственна.
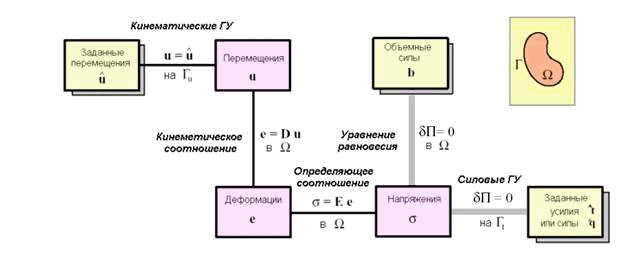
Рис. 9.54. Ослабленная
формулировка задач теории упругости в виде диаграммы Тонти.
На рис. 9.54 представлена ослабленная формулировка
плоской задачи теории упругости, связанная с вариационным принципом минимума
полной потенциальной энергии тела. Согласно данной формулировке уравнение
равновесия в области и силовые граничные условия на части поверхности Гt выполняются в ослабленном смысле
как вариационные соотношения принципа минимума полной потенциальной энергии ![]() , где функционал энергии П будет
подробно рассмотрен ниже. Соответствующие связи выражены серыми линиями.
Формулировка метода конечных элементов в перемещениях основывается на данной
ослабленной формулировке задачи.
, где функционал энергии П будет
подробно рассмотрен ниже. Соответствующие связи выражены серыми линиями.
Формулировка метода конечных элементов в перемещениях основывается на данной
ослабленной формулировке задачи.
9.7.7.2. Полная
потенциальная энергия тела
Функционал полной потенциальной энергии идеально
упругого тела определяется следующей формулой:
![]() .
(9.25)
.
(9.25)
В соотношении (9.25) U есть внутренняя энергия
деформации тела, вычисляемая как интеграл по объему тела от удельной энергии
деформации тела, равной половине матричного произведения вектора напряжений на
вектор деформаций:
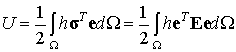 .
(9.26)
.
(9.26)
Толщина h появляется
под знаком интеграла в результате представления объемного интеграла через
повторный интеграл по области ![]() и нормальной
координате z:
и нормальной
координате z:
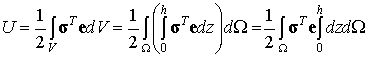 .
.
Поскольку напряжения и деформации не зависят от
координаты z согласно постановке плоской задачи
теории упругости, то их произведение может быть вынесено за знак интеграла по
толщине пластины h. Заметим, что сама толщина
может быть переменной в области пластины, и поэтому полностью за знак интеграла
не выносится.
Величина A в формуле (9.25) представляет собой
работу внешних объемных и поверхностных сил, заданных
соответственно в области ![]() и на части поверхности
Гt.:
и на части поверхности
Гt.:
![]() .
(9.27)
.
(9.27)
Аналогично предыдущему объемный
интеграл от объемных сил преобразуется к повторному и затем в результате
интегрирования по толщине - к интегралу по области пластины![]() . Второй интеграл, представляющий собой работу поверхностных
сил, действующих на боковой грани пластины преобразуется сходным образом:
. Второй интеграл, представляющий собой работу поверхностных
сил, действующих на боковой грани пластины преобразуется сходным образом:
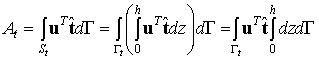 .
.
Обратим внимание, что в соотношении (9.27)
используется интеграл только по части поверхности Гt, поскольку только на данной части
поверхности заданы внешние силы.
9.7.7.3.
Конечно-элементная интерполяция
Согласно основной идее метода конечных элементов
область тела ![]() представляется в виде
множества непересекающихся подобластей, называемых конечными элементами, как
показано на рис. 9.55.
представляется в виде
множества непересекающихся подобластей, называемых конечными элементами, как
показано на рис. 9.55.
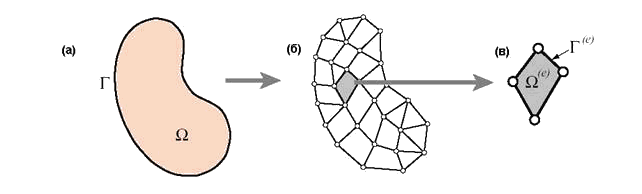
Рис. 9.55.
Конечно-элементная дискретизация области тела: (а) – исходная область ![]() с границей Г; (б) – дискретизованная
область
с границей Г; (б) – дискретизованная
область![]() , представленная в виде сетки конечных элементов; (в) –
конечный элемент, занимающий область
, представленная в виде сетки конечных элементов; (в) –
конечный элемент, занимающий область ![]() с границей Г(е).
с границей Г(е).
Как правило, для решения плоской задачи теории
упругости используются трехсторонние или четырехсторонние конечные элементы.
Каждый конечный элемент определяется набором узлов. В качестве примера на рис.
9.55 приведен четырехсторонний элемент с линейной интерполяцией координат и
перемещений, заданный четырьмя узлами. Напомним, что в случае использования
квадратичной интерполяции координат или перемещений четырехсторонний элемент
должен описываться восемью узлами (Рис. 9.14).
В случае плоской задачи в каждом узле заданы две
компоненты перемещений, которые являются искомыми степенями свободы, как
говорилось в предыдущих лекциях. Искомые степени свободы, или узловые
переменные, принято объединять в так называемые элементные вектора узловых переменных,
в данном случае узловых перемещений:
![]() .
(9.28)
.
(9.28)
Таким образом, каждый элементный вектор содержит 2n степеней свободы, где n – число узлов элемента. В данном случае
n=4 (Рис. 9.55), однако, как было
показано в разделе 9.5, число узлов может быть различным в зависимости от типа
элемента (Рис. 9.56). Заметим также, что, пронумеровав узлы от 1 до n в пределах
данного элемента, мы тем самым ввели локальную нумерацию узлов на
элементе. Необходимо отметить, что способ нумерации узлов в пределах элемента
может быть произвольным. Однако, один раз выбрав способ нумерации для данного
типа элементов, необходимо его придерживаться.
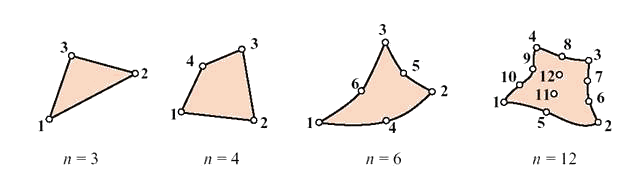
Рис. 9.56. Примеры
двумерных конечных элементов, определяемых различным числом узлов.
После выбора узловых переменных необходимо задать
закон изменения искомой функции в пределах конечного элемента. Поле перемещений
в пределах элемента определяются с помощью интерполирующих соотношений:
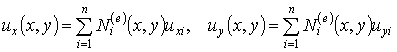 , (9.29)
, (9.29)
где ![]() - специальные
интерполирующие функции, или функции формы элемента.
- специальные
интерполирующие функции, или функции формы элемента.
Эти функции обладают рядом специфических свойств,
которые будут рассматриваться в дальнейшем. Одно из основных свойств, которое
хотелось бы отметить сейчас – локальность, или финитность
интерполирующих функций, что означает, что эти функции заданы только в пределах
данного элемента. Заметим также, что функции формы играют значительную роль в
алгоритме метода конечного элемента, поскольку задают порядок интерполяции
искомых переменных.
Минимальное условие, которое должно быть наложено на
функции![]() , то, что каждая функция
, то, что каждая функция ![]() должна принимать единичное значение в узле i элемента, и обращаться в ноль в остальных узлах.
должна принимать единичное значение в узле i элемента, и обращаться в ноль в остальных узлах.
В матричной форме интерполирующие соотношения (9.29)
могут быть записаны следующим образом:
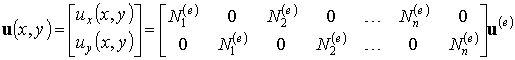 , (9.30а)
, (9.30а)
откуда получаем:
![]() .
(9.30б)
.
(9.30б)
В соотношениях (9.30а) и (9.30б) ![]() представляет собой
матрицу интерполирующих функций размерности 2x2n, поскольку мы рассматривает двумерную задачу. В случае трехмерной
задачи теории упругости соответствующая матрица интерполирующих функций имела
бы размерность 3x3n. При этом вид
соотношения (9.30б) не изменился бы. В этом проявляется значительное
достоинство метода конечных элементов: основные формулы общего алгоритма
остаются справедливыми и не меняют своего вида при анализе различных задач
теории упругости.
представляет собой
матрицу интерполирующих функций размерности 2x2n, поскольку мы рассматривает двумерную задачу. В случае трехмерной
задачи теории упругости соответствующая матрица интерполирующих функций имела
бы размерность 3x3n. При этом вид
соотношения (9.30б) не изменился бы. В этом проявляется значительное
достоинство метода конечных элементов: основные формулы общего алгоритма
остаются справедливыми и не меняют своего вида при анализе различных задач
теории упругости.
Соотношение (9.30б) является одним из наиболее важных
фундаментальных уравнений метода конечных элементов, поскольку участвует при
выводе практически всех формул алгоритма МКЭ. В частности, теперь с помощью
данного уравнения мы можем преобразовать кинематическое соотношение (9.18а),
входящее в постановку плоской задачи теории упругости и связывающее перемещения
и деформации в точке. В матричном виде данное соотношение в произвольной точке
конечного элемента может быть записано следующим образом:
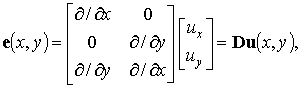 (9.31а)
(9.31а)
где D – матрица, состоящая из частных
производных интерполирующих функций по пространственным координатам.
Подставляя в соотношение (9.31а) интерполирующее
соотношение (9.30б), получим:
![]() ,
(9.31б)
,
(9.31б)
где ![]() -
представляет собой матрицу размерности 3x2n,
называемую матрицей градиентов.
-
представляет собой матрицу размерности 3x2n,
называемую матрицей градиентов.
Явное выражение матрицы градиентов может
быть получено, если мы перемножим матрицу D размерности
3x2 на матрицу ![]() размерности 2x2n. В результате получим:
размерности 2x2n. В результате получим:
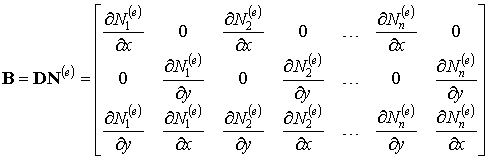 . (9.32)
. (9.32)
В развернутом виде выражение деформации в точке, таким
образом, может быть записано в виде:
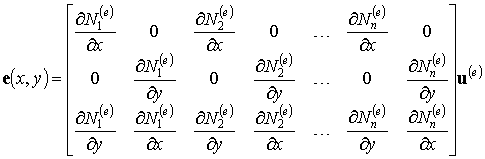 . (9.33)
. (9.33)
Заметим, что матрица градиентов, также как и матрица
интерполирующих функций зависит от номера элемента e.
В данном случае индекс e опущен только для
сокращения записи.
После определения вектора деформации в точке можно
вычислить и вектор напряжений согласно формуле (9.18б). В матричном виде она
может быть представлена следующим образом:
![]() .
(9.34)
.
(9.34)
Данное соотношение выполняется во всех точках
конечного элемента и поэтому вместо вектора деформации e(x,y) может быть
подставлено его выражение (9.31б). В результате получим:
![]() . (9.35)
. (9.35)
Таким образом, пользуясь основным интерполяционным
соотношением МКЭ, мы получили необходимые выражения векторов деформаций и
напряжений в произвольной точке произвольного конечного элемента. Эти формулы
существенным образом будут использованы в следующей лекции при выводе
разрешающих уравнений метода конечных элементов применительно к плоской задаче
теории упругости.
email: KarimovI@rambler.ru Адрес: Россия, 450071, г.Уфа, почтовый ящик 21