Главная
9.14.
Формирование векторов узловых сил изопараметрического
элемента
9.14.1.
Введение
В настоящей лекции будет
подробно рассмотрен алгоритм формирования элементного вектора узловых сил,
статически эквивалентного заданным объемным силам 
(9.62), и элементного
вектора узловых сил, статически эквивалентного заданным поверхностным силам 
(9.63):
(9.173)
(9.174)
где b - заданный вектор объемных сил;
- заданный вектор поверхностных сил;
- толщина элемента е;
- площадь элемента е;
- граница
элемента е;
Ne - матрица интерполирующих функций, или функций формы элемента.
9.14.2.
Структура элементных векторов сил
Рассмотрим структуру выражений (9.173) и (9.174). Аналогично предыдущей лекции все определяется подынтегральным выражением, которое имеет сходную форму для обоих типов элементных векторов. Поэтому достаточно подробно рассмотреть только одно из них, например (9.173).
Раскроем подынтегральное произведение (формулы (9.30) и (9.18в)):
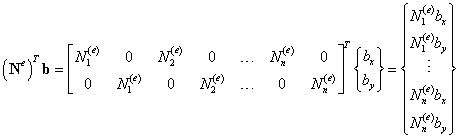(9.175)
Подставляя полученный матричный вектор (9.175), в формулу (9.173) получим выражение элементного вектора узловых сил, статически эквивалентного заданным объемным силам:
,
(9.176)
где компоненты вектора имеют вид:
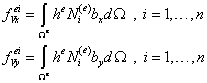(9.177)
Аналогично рассуждая, найдем выражение элементного вектора узловых сил, статически эквивалентного заданным поверхностным силам:
,
(9.178)
где компоненты вектора имеют вид:
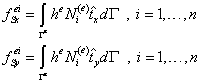(9.179)
9.14.3.
Вычисление компонент элементного вектора объемных сил
Компоненты элементного вектора объемных сил (9.177) вычисляются путем перехода к повторному интегралу аналогично вычислению элементных матриц жесткости, подробно рассмотренному в лекции 9.13:
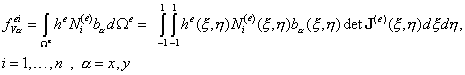(9.180)
Применения к (9.180) квадратуры Гаусса, в результате получим окончательное выражение для вычисления компонент элементного вектора объемных сил:
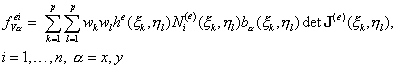(9.181)
Заметим, что как толщина элемента, так и вектор объемных сил также могут быть заданы с помощью изопараметрических соотношений через свои узловые значения:
,
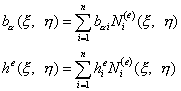(9.181а)
где 
- значение заданной
силы в узле i конечного элемента;
- значение толщины элемента е в узле i.
Это особенно удобно при разработке универсальных программных комплексов для унификации ввода данных.
9.14.4.
Вычисление компонент элементного вектора поверхностных сил
Вычисление компонент элементного вектора
поверхностных сил (9.179) значительно отличается от вычисления интегралов от
объемных сил ввиду того, что необходимо интегрировать по границе элемента Гe.
Границей плоской области является кривая линия на плоскости. В данном случае
границей области элемента будут четыре его
стороны. Следовательно, в самом общем случае, который чаще всего не реализован
на практике, необходимо вычисление интегралов по каждой из сторон элемента:
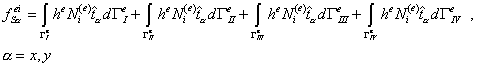(9.182)
где 
- стороны
элемента е.
Не умаляя общности, достаточно рассмотреть вычисление лишь одного из интегралов, входящих в сумму (9.182). Возьмем для определенности интеграл по первой стороне четырехстороннего изопараметрического элемента (Рис. 9.75).
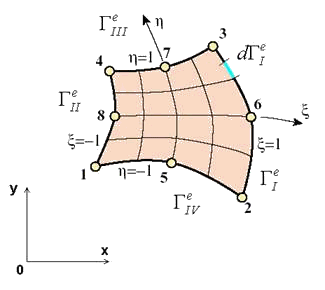
Рис.
9.75. Граница Гe четырехстороннего конечного элемента, образованная четырьмя
сторонами, и бесконечно малый элемент дуги 
.
Как уже было отмечено, стороны элемента, по
определению, совпадают с координатными линиями локальной естественной системы
координат (см. лекцию 9.11): 
и 
. Следовательно, параметрическое представление кривой 2-3,
совпадающей с первой стороной элемента и описываемой уравнением 
в локальной системе
координат, имеет вид:
(9.183)
Принимая во внимание изопараметрические соотношения (9.125), уравнение первой стороны элемента виде может быть представлено следующим образом:
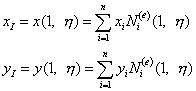(9.184)
Вычислим теперь дифференциал дуги , имеющий математический смысл длины бесконечно малого элемента
кривой 2-3. С точностью до величин второго и высших порядков малости, элемент является отрезком
прямой линии в плоскости 
, длина которого находится из простого тригонометрического
соотношения как гипотенуза прямоугольного треугольника:
,
(9.185)
где 
, 
- проекции отрезка на оси глобальной
системы координат, они же дифференциалы координат кривой линии 2-3, заданной в
параметрическом виде (9.184).
Дифференцируя уравнения (9.184) и подставляя
найденные значения , в (9.185), получим
выражение дифференциал дуги :
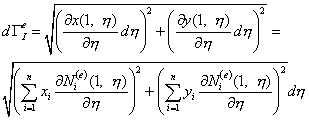(9.186)
Ведем обозначение функции:
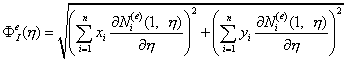, (9.187)
имеющей смысл якобиана преобразования между
координатами точек кривой, заданной в локальной системе координат уравнением , и в глобальной системе координат уравнением
(9.184). Другая, но близкая по сути,
интерпретация функции (9.187) – якобиан отображения кривой 2-3 на отрезок
прямой 
.
После того, как получено выражение
дифференциал дуги , можно перейти от криволинейного интеграла по стороне
элемента 
к обыкновенному
определенному интегралу от функций, зависящих от одной скалярной переменной:
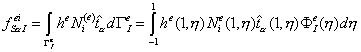(9.188)
9.14.5.
Численное интегрирование
Применения к (9.188) квадратуры Гаусса, в результате получим окончательное выражение для вычисления компонент элементного вектора поверхностных сил, заданных на первой стороне конечного элемента:
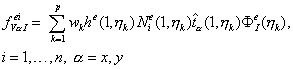(9.189)
Заметим, что вектор поверхностных сил может быть задан с помощью аналогичных изопараметрических соотношений через свои узловые значения. Однако, в этом случае необходимо использовать одномерные функции формы:
, (9.189а)
где 
- значение заданной силы в узле i
конечного элемента;
- одномерные функции
формы;
- число узлов на стороне конечного элемента.
Аналогично вычисляются остальные интегралы, входящие в общее выражение элементного вектора узловых поверхностных сил (9.182). Приведем эти формулы без вывода для полноты изложения (см. рис. 9.75 для пояснения используемой нумерации сторон конечного элемента):
Сторона II, узлы 4-1, уравнение 
:
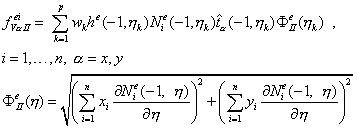(9.190)
Сторона III, узлы 3-4, уравнение 
:
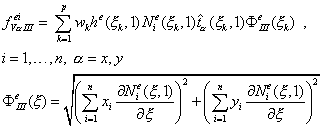(9.191)
Сторона IV, узлы 1-2, уравнение 
:
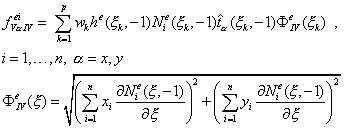(9.192)
Таким образом, можно сделать вывод, что сформированы все необходимые элементные вектора заданных объемных и поверхностных сил, а также элементные матрицы жесткости. Как правило, это является одним из самых сложных этапов при разработке программной реализации метода конечных элементов. Вторым важным этапом будет сборка глобальных матриц жесткости и векторов нагрузки, формирование системы линейных алгебраических уравнений и решение СЛАУ.
email: KarimovI@rambler.ru Адрес: Россия, 450071, г.Уфа, почтовый ящик 21
