Главная
9.18.
Теоретические основы метода граничных элементов
9.18.1.
Введение
Численные методы механики деформируемого твердого тела могут быть разделены на три основных вида: метод конечных разностей, метод конечных элементов и метод граничных элементов (более общее название – метод граничных интегральных уравнений).
Первый из этих методов связан с непосредственной реализацией разностного оператора, соответствующего исходному дифференциальному уравнению задачи. Данный подход обладает одним существенным свойством: он позволяет легко распространить методику на решение нелинейных задач и не требует сложных математических преобразований. К сожалению, точность получаемых результатов оказывается невысокой.
Метод конечных элементов базируется на разбиении исследуемого тела на ряд подобластей простого очертания, называемых конечными элементами. В основе численной модели лежат вариационные принципы механики, наиболее часто принцип минимума потенциальной энергии. Механическая ясность и широкие практические возможности метода объясняют его популярность среди исследователей.
Однако существует много классов задач, для которых конечно-элементная реализация неудовлетворительна, что и заставило ученых обратиться к альтернативным методам, основывающимся на интегральных уравнениях.
В данном курсе лекций мы рассмотрим один из таких подходов – прямой метод граничных элементов. Сначала изложим математическую базу метода: исходная система дифференциальных уравнений пространственной задачи теории упругости преобразуется в граничное интегральное уравнение относительно неизвестных поверхностных перемещений и напряжений. Для численного решения этого уравнения вся поверхность тела разбивается на ряд элементов, в пределах которых перемещения и напряжения интерполируются с помощью полимиальных функций через их значения в узловых точках. Далее опишем программы для численного решения плоских задач теории упругости и рассмотрим тестовый пример на применение данной программы.
В лекциях будем использовать декартовое
тензорное обозначение, в соответствии с которым для представления осей 
используются индексы (1, 2, 3). Кроме того, необязательны
символы суммирования, если в слагаемом одни и те же нижние индексы встречаются
дважды. Например,
,
.
В данной лекции будет показано, как задача теории упругости, сформулированная в идее полной системы уравнений линейной теории упругости с граничными условиями, может быть сведена к интегральному уравнению, допускающую численную реализацию в рамках прямого метода граничных элементов.
9.18.2.
Постановка пространственной задачи теории упругости
Рассмотрим тело 
(
- граница области 
) (Рис. 9.80), которое находится в состоянии равновесия под
воздействием заданных нагрузок и перемещений. Это состояние описывается полной
системой уравнений линейной теории упругости:
,
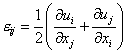, (9.224)
,
где
- компоненты тензора напряжений;
- компоненты тензора деформаций;
- компоненты вектора перемещений;
- компоненты вектора объемных сил;
- символ Кронекера, 
; 
; 
;
- объемная деформация, 
;
- коэффициент Пуассона;
- модуль сдвига.
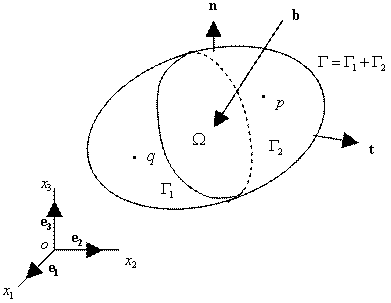
Рис. 9.80. Постановка пространственной задачи теории упругости.
Граничные условия имеют вид:
, (9.224а)
где
- компоненты вектора напряжений на границе;
- компоненты вектора нормали к поверхности;
- часть границы, на которой заданы кинематические условия;
- часть границы, на которой заданы силовые условия.
9.18.3.
Вывод интегрального уравнения задачи
Вывод интегрального уравнения основан на преобразовании дифференциальных уравнений теории упругости в интегральные уравнения. Это может быть осуществлено с помощью теоремы Бетти о взаимности работ. Рассматриваются два состояния упругой среды:
1: 
2: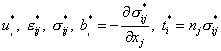 
.
Оба состояния должны удовлетворять уравнению
равновесия в под действием заданных
объемных сил, поверхностных нагрузок и перемещений.
Пусть 1-е состояние определяется исходной постановкой
задачи. В качестве второго возьмем следующее состояние упругой среды: область 
с границей 
, которая включает в себя рассматриваемое тело (рис. 9.81).
Считается, что и эта область находится в состоянии равновесия, обозначенном
символом «*». Пусть теперь в качестве вектора объемных сил b*k
выступают единичные сосредоточенные усилия, приложенные в точке 
в каждом из трех
ортогональных направлений ek,
т.е.
или
,
,
,
где 
- дельта-функция Дирака.
Возникающие поля перемещений и напряжений
можно вычислить как решение полной системы уравнений теории упругости или
эквивалентного ей уравнения Навье в области 
:
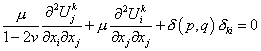, (9.225)
где 
- i-я
компонента вектора перемещений в точке q, от действия в точке p единичной
сосредоточенной силы в направлении ek.
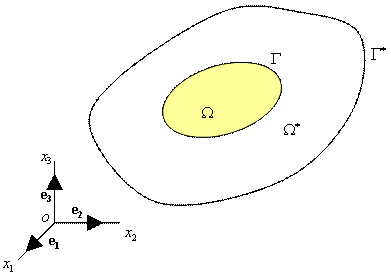
Рис.
9.81. Область 
с границей 
, которая включает в себя рассматриваемое тело .
Решения этого уравнения называются фундаментальными
сингулярными решениями. Они образуют тензоры фундаментальных решений U
и T с компонентами: , 
- i-я
компонента вектора перемещений (напряжений) в точке q,
вызванная действием единичной сосредоточенной силы в точке p в
направлении ek.
.
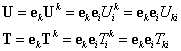Тогда перемещения и напряжения в любой точке q тела при действии сосредоточенной единичной силы в точке p в направлении l определяется так:
.
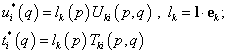Теперь отсекаем область 
, и действие отброшенной части заменяем распределенными
поверхностными нагрузками и перемещениями на границе :
.
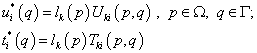Оставшаяся часть области находится в равновесии
и описывается следующими параметрами:
.
Теперь для области можно записать теорему
Бетти:
.
Подставляя 
, 
, 
в уравнение взаимности
работ, получаем:
.
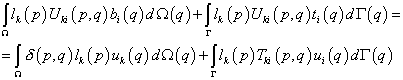Используя фильтрующее свойство 
-функции
,
получим интегральное уравнение задачи:
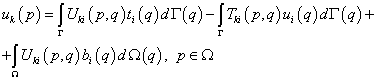. (9.226)
Это выражение называется также тождеством Сомильяны для перемещений. Перейдем от тензорной формы записи к матричной:
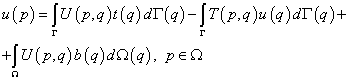, (9.226а)
где u, t, b – векторы столбцы; U, T – матрицы. Их размерность: dim u = dim t = dim b =3x1, dim U = dim T = 3x3.
9.18.4.
Граничное интегральное уравнение
Согласно концепции метода граничных элементов рассматривается предельная форма интегрального уравнения (9.226а) при перемещении точки p к границе. Тогда (9.226а) приобретает вид:
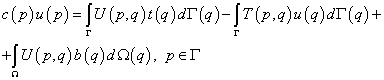, (9.227)
где c(p) – матрица, зависящая от гладкости границы Г в окрестности точки p.
Уравнение (9.227) справедливо как для трех-, так и для двухмерных задач, и представляет собой соотношение, которое должно выполняться между перемещениями и напряжениями на поверхности тела, а также объемными силами. Поскольку объемные силы известны, видно, что это граничное интегральное уравнение (ГИУ) относительно неизвестных граничных значений перемещений и усилий.
email: KarimovI@rambler.ru Адрес: Россия, 450071, г.Уфа, почтовый ящик 21
