Главная
9.19.
Численная реализация метода граничных элементов
9.19.1.
Гранично-элементная дискретизация
Решить ГИУ аналитически для произвольной области не представляется возможным. Поэтому применяется гранично-элементная дискретизация, аналогичная процедура МКЭ. Граница Г представляется серией граничных элементов (ГЭ) Ге, на каждом из которых перемещения и поверхностные усилия получаются интерполированием по узловым точкам элемента. Интегральный член с объемными силами опустим, т.к. для сути МГЭ он не имеет принципиального значения.
Дискретизованная модель границы области (Рис. 9.82) характеризуется глобальными векторами координат узлов X:
![]() ,
,
где ![]() - вектор координат узла
- вектор координат узла ![]() . Вектор координат узлов ГЭ Ге
получается из глобального вектора координат при помощи матрицы кинематической
связи:
. Вектор координат узлов ГЭ Ге
получается из глобального вектора координат при помощи матрицы кинематической
связи:
![]() .
.
Координаты любой внутренней точки ГЭ Ге определяются с помощью матрицы интерполирующих функций
![]() , (9.228)
, (9.228)
где ![]() - локальная система
координат ГЭ:
- локальная система
координат ГЭ: ![]() .
.

Рис. 9.82. Дискретизованная модель границы области (поверхности тела).
Аналогично в случае изопараметрического элемента определяются перемещения и поверхностные усилия через векторы узловых перемещений и усилий на ГЭ Ге:
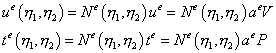 , (9.229)
, (9.229)
где V, P – глобальные векторы перемещений и усилий.
После разбиения границы на элементы ГИУ (9.227) принимает вид:
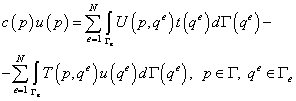 . (9.230)
. (9.230)
В это выражение входят поверхностные интегралы по ГЭ Ге.
Элемент поверхности может быть записан так:
![]() ,
,
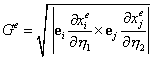 ,
,
где ![]() - якобиан преобразования от глобальной к локальной
системе координат.
- якобиан преобразования от глобальной к локальной
системе координат.
Подставляя в дискретизованное
ГИУ выражение для ![]() и интерполяционные
соотношения для перемещений и усилий, получим:
и интерполяционные
соотношения для перемещений и усилий, получим:
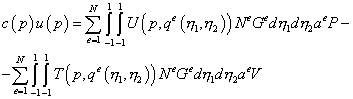 . (9.231)
. (9.231)
9.19.2.
Формирование системы линейных алгебраических уравнений
В уравнении (9.231) точка p расположена
на границе произвольно. Согласно методу коллокаций выберем
ее совпадающей последовательно с каждым из узлов границы. В результате получаем
систему матричных уравнений (![]() - глобальное число узлов границы):
- глобальное число узлов границы):
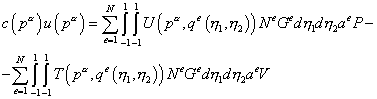 , (9.232)
, (9.232)
где ![]() - глобальный номер
узла.
- глобальный номер
узла. ![]() .
.
Последнее уравнение можно переписать в матричном виде:
![]() ,
(9.233)
,
(9.233)
где
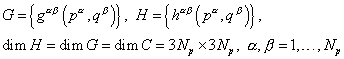 ,
,
где ![]() - матричный блок
размерностью 3x3, который представляет собой сумму интегральных вкладов с
ядрами
- матричный блок
размерностью 3x3, который представляет собой сумму интегральных вкладов с
ядрами ![]() от всех ГЭ, содержащих
узел с номером
от всех ГЭ, содержащих
узел с номером ![]() , а точка коллокации совпадает с
узлом
, а точка коллокации совпадает с
узлом ![]() , т.е. этот матричный блок характеризует влияние узла
, т.е. этот матричный блок характеризует влияние узла ![]() на узел с номером
на узел с номером![]() .
.
В уравнение (9.233) входят как известные из граничных условий перемещения и усилия, так и неизвестные, поэтому удобно разделить векторы V и P на известную часть и неизвестную:
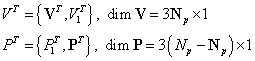 .
.
То есть в ![]() узлах заданы
перемещения, а в
узлах заданы
перемещения, а в ![]() - усилия.
- усилия.
Соответствующим образом разделяются и компоненты матриц G и С+Н. Перенеся вектор известных величин в правую часть, получим окончательный вид системы линейных алгебраических уравнений метода граничных элементов:
![]() ,
(9.234)
,
(9.234)
где ![]() - вектор неизвестных поверхностных
усилий и перемещений,
- вектор неизвестных поверхностных
усилий и перемещений, ![]() - полностью заполненная матрица размерности
- полностью заполненная матрица размерности ![]() .
.
Как только все узловые граничные значения перемещений и усилий становятся известными в результате решения СЛАУ, то могут быть вычислены перемещения и напряжения внутри тела с помощью соответствующих дискретизованных уравнений. Напряжения в граничных узлах определяются по значениям перемещений и усилий на границе с использованием дифференцирования в пределах ГЭ.
9.19.3.
Особенности математической формулировки МГЭ для решения плоских задач теории
упругости
Граничное интегральное уравнение (9.227),
выведенное в лекции 9.18 для пространственного случая, полностью сохраняет свой
вид и для плоской задачи. Однако при гранично-элементной дискретизации следует
учитывать, что область ![]() - есть двумерное плоское упругое тело, а граница Г -
есть контур этого тела (рис. 9.83). В многих
разрабатываемых программах для моделирования кривой линии и распределения
перемещения и усилий вдоль нее используются так называемые линейные элементы,
функции формы которых имеют вид (рис. 9.84):
- есть двумерное плоское упругое тело, а граница Г -
есть контур этого тела (рис. 9.83). В многих
разрабатываемых программах для моделирования кривой линии и распределения
перемещения и усилий вдоль нее используются так называемые линейные элементы,
функции формы которых имеют вид (рис. 9.84):
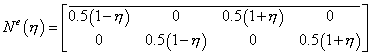 , (9.235)
, (9.235)
а вектор координат узлов ГЭ Ге (рис. 9.83)
![]() .
.

Рис. 9.83. Гранично-элементная дискретизация границы плоской области.
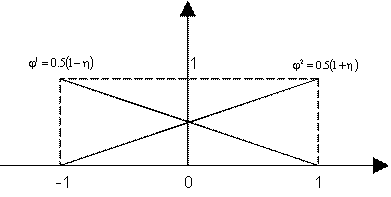
Рис. 9.84. Функции формы одномерного линейного изопараметрического элемента.
В силу этого интегрирование по граничному
элементу будет означать интегрирование по отрезку ![]() , а окончательная СЛАУ приобретает размерность
, а окончательная СЛАУ приобретает размерность ![]() .
.
Здесь же приведем вид фундаментальных решений для плоской бесконечной области:
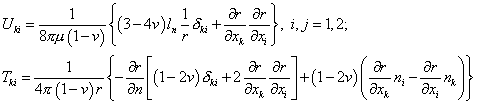 , (9.236)
, (9.236)
где ![]() – расстояние между
точкой коллокации
– расстояние между
точкой коллокации
![]() и произвольной точкой на ГЭ,
и произвольной точкой на ГЭ, ![]() - символы Кронекера.
- символы Кронекера.
Как видно из рисунка 20.2, расстояние ![]() есть модуль вектора,
соединяющего точки
есть модуль вектора,
соединяющего точки ![]() и
и ![]() :
:
![]() ,
,
тогда можно вычислить производные расстояния
![]() по координате
по координате ![]() следующим образом:
следующим образом:
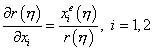 .
.
В выражении ![]() фигурирует производная
расстояния
фигурирует производная
расстояния ![]() по нормали к границе
по нормали к границе ![]() . Она вычисляется согласно правилу определения
производной скалярной функции по направлению:
. Она вычисляется согласно правилу определения
производной скалярной функции по направлению:
![]() .
.
Приведенное фундаментальное решение (9.236)
носит название решение Кельвина - Сомильяны. Оно получается как решение уравнения Навье (9.225) в случае, когда ![]() представляет собой
бесконечную область, в произвольной точке
представляет собой
бесконечную область, в произвольной точке ![]() которой действует единичная сосредоточенная сила в
направлении координатной оси
которой действует единичная сосредоточенная сила в
направлении координатной оси ![]() или
или ![]() . Важнейшая особенность такого решения заключается в том, что
перемещения и усилия, определяемые формулами (9.236), неограниченно возрастают при
приближении точки
. Важнейшая особенность такого решения заключается в том, что
перемещения и усилия, определяемые формулами (9.236), неограниченно возрастают при
приближении точки ![]() , в которой они вычисляются, к точке
, в которой они вычисляются, к точке ![]() , в которой приложена сосредоточенная сила, т.е.
, в которой приложена сосредоточенная сила, т.е.
![]()
при
![]() .
.
Поэтому решения такого вида называются сингулярными
решениями, а точка ![]() - сингулярной точкой
- сингулярной точкой![]() .
.
email: KarimovI@rambler.ru Адрес: Россия, 450071, г.Уфа, почтовый ящик 21